Multiple Regression

May 19, 2025

Load packages

library(tidyverse)
library(dplyr)
library(ggplot2)
library(tidymodels)
library(patchwork)
library(DT)
library(vdemdata)

Load VDEM Data

modelData <- vdem %>% 
  filter(year == 2019) %>% 
  select(country_name, v2x_libdem, e_gdppc, v2cacamps, e_total_oil_income_pc, v2x_corr) %>% 
  mutate(lg_gdppc = log(e_gdppc))

Linear Model with Multiple Predictors


  • Previously, we were interested in GDP per capita as a predictor of democracy.

  • Now, let’s consider another predictor: polarization (also measured by V-Dem)

Polarization Measure in the USA

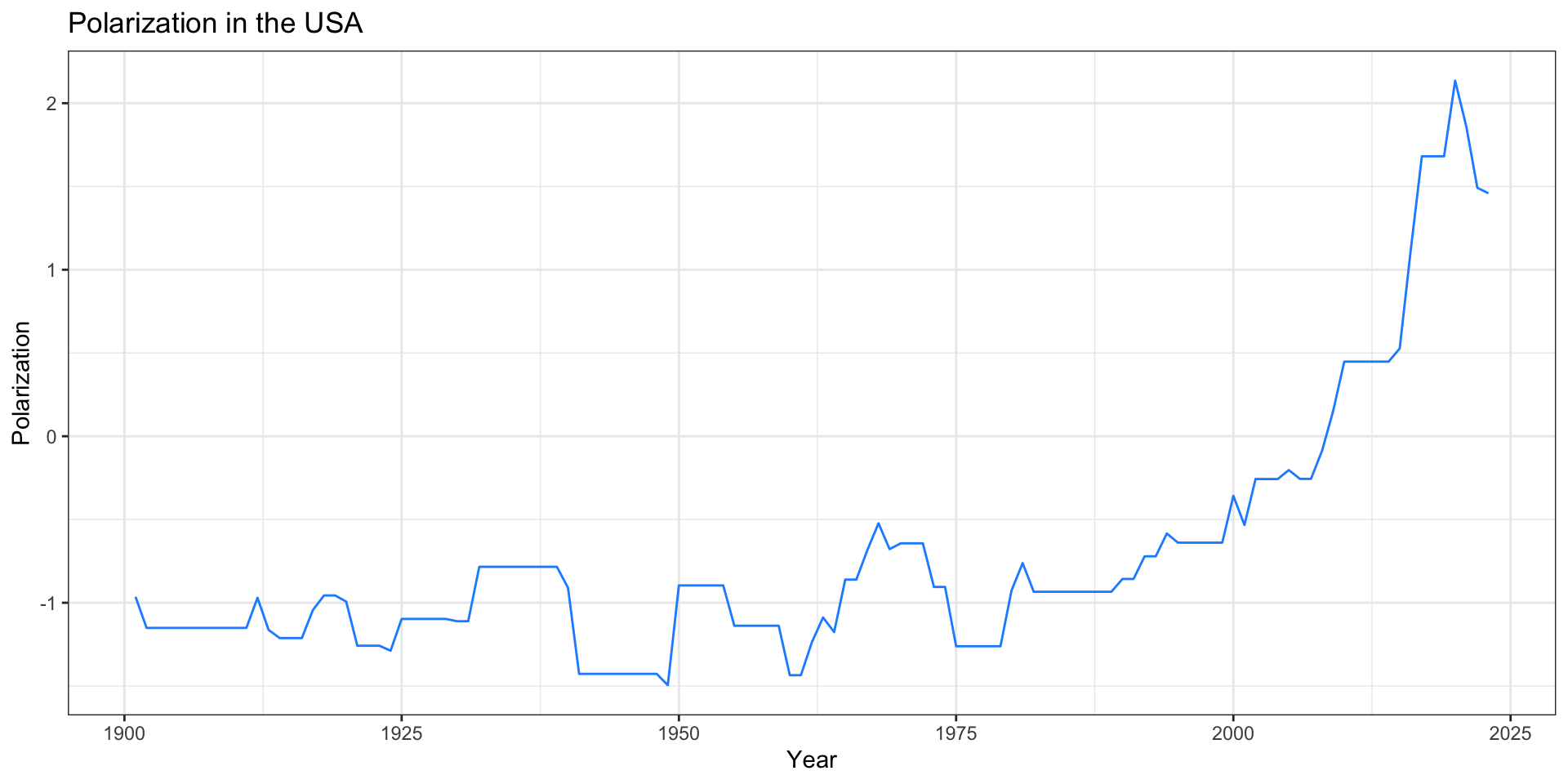
Polarization and Democracy in 2019

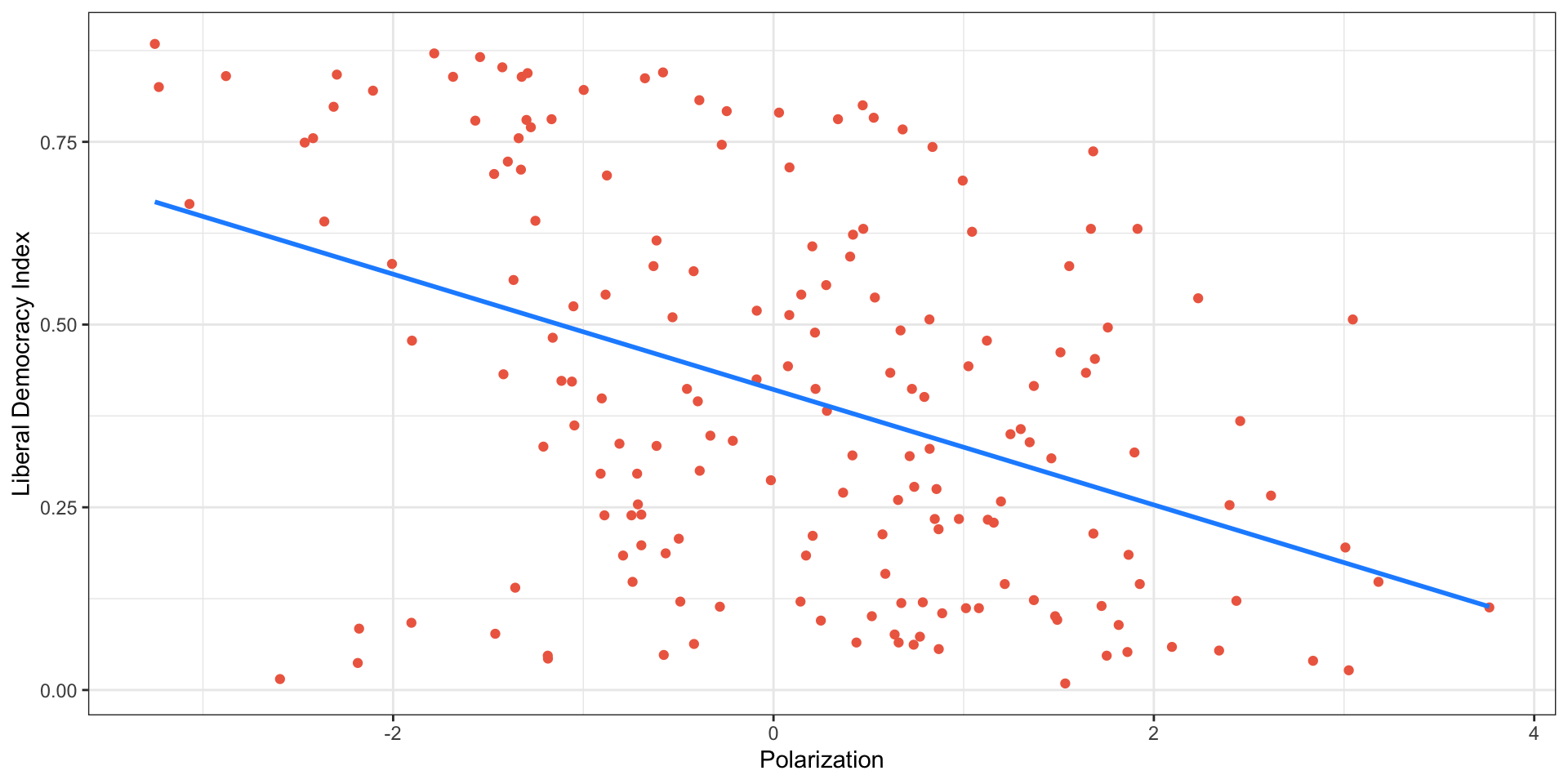
Model with Polarization as the only Predictor


How do we interpret the intercept and the slope estimate?

linear_reg() %>%
  set_engine("lm") %>%
  fit(v2x_libdem ~ v2cacamps, data = modelData) %>% 
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   0.411     0.0178     23.2  1.94e-55
2 v2cacamps    -0.0789    0.0126     -6.27 2.66e- 9

How are we figuring out what the “best” line is?

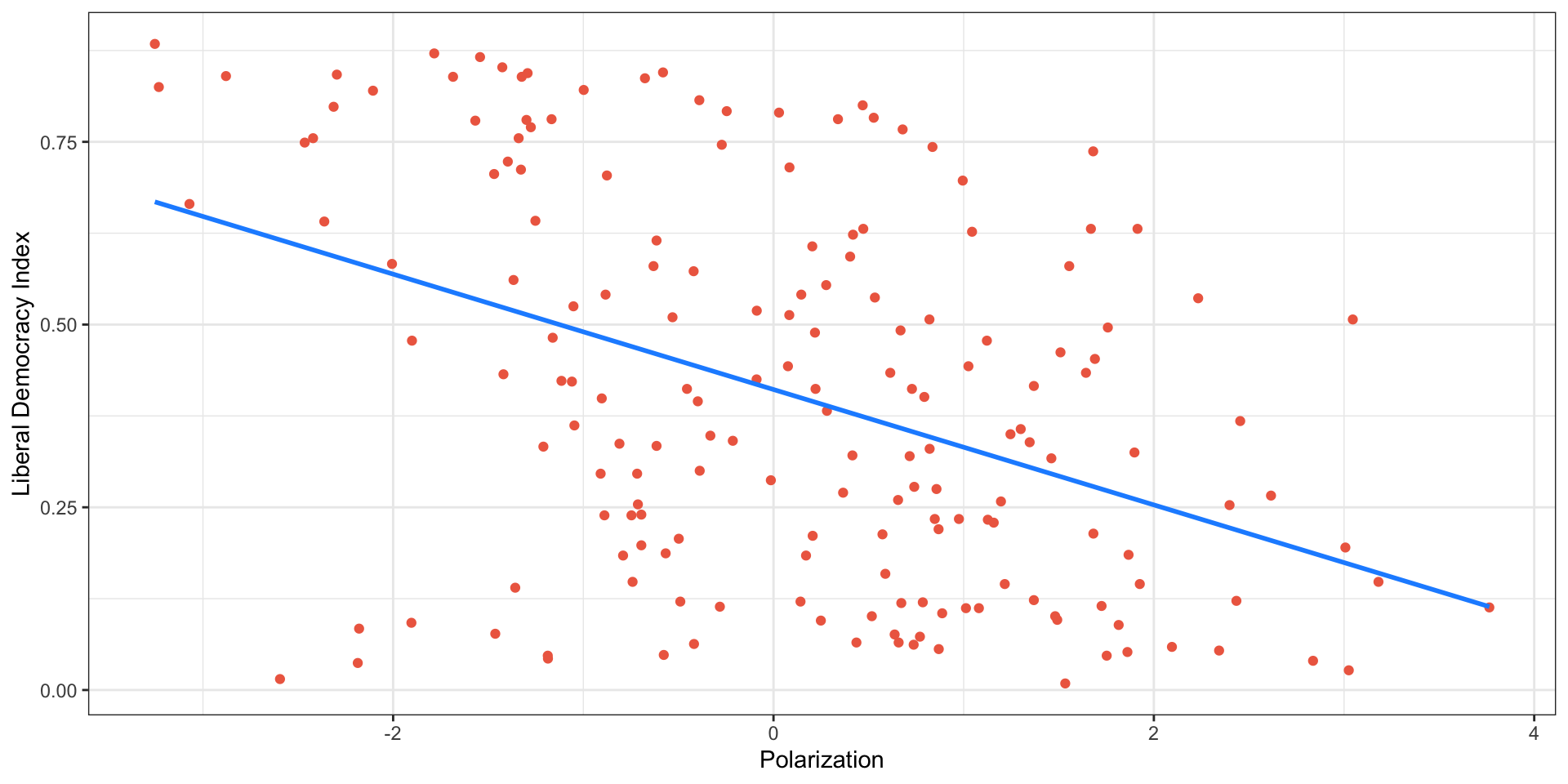
Model with Two Predictors


\[\hat{Y_i} = a + b_1*Polarization + b_2*GDPpc\]

  • OLS is searching for combination of \(a\), \(b_1\), and \(b_2\) that minimize sum of squared residuals

    • same logic as model with one predictor, just more complicated

Model with Two Predictors

linear_reg() %>%
  set_engine("lm") %>%
  fit(v2x_libdem ~ v2cacamps + lg_gdppc, data = modelData) %>% 
  tidy()
# A tibble: 3 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   0.182     0.0378      4.81 3.32e- 6
2 v2cacamps    -0.0539    0.0120     -4.51 1.19e- 5
3 lg_gdppc      0.100     0.0147      6.82 1.50e-10

Model with Two Predictors

\[\hat{Y_i} = a + b_1*Polarization + b_2*GDPpc\]

\[\hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc\]

Model with Two Predictors

\[\hat{Y_i} = a + b_1*Polarization + b_2*GDPpc\]

\[\hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc\]

  • \(a\) is the predicted level of Y when BOTH GDP per capita and polarization are equal to 0

Model with Two Predictors

\[\hat{Y_i} = a + b_1*Polarization + b_2*GDPpc\]

\[\hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc\]

  • \(b_1\) is the impact of a 1-unit change in polarization on the predicted level of Y, holding GDP per capita fixed (all else equal)

    • The relationship between polarization and democracy, controlling for GDP per capita.

Model with Two Predictors

\[\hat{Y_i} = a + b_1*Polarization + b_2*GDPpc\]

\[\hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc\]

  • \(b_2\) is the impact of a 1-unit change in GDP per capita on the predicted level of Y, holding polarization fixed (all else equal)

Posit Cloud Practice

library(peacesciencer)

conflictData <- create_stateyears(system = 'gw') %>% 
  filter(year %in% c(1946:1999)) %>%
  add_ucdp_acd(type=c("intrastate"), only_wars = FALSE) %>%
  add_democracy() %>% ## adds democracy measures 
  add_creg_fractionalization() %>% ## adds ethnicity and religious fractionalization
  mutate(democracy = ifelse(v2x_polyarchy > .5, "Democracy", "Autocracy"))

linear_reg() %>%
  set_engine("lm") %>%
  fit(ucdponset ~ democracy + ethfrac, data = conflictData) %>% 
  tidy()
# A tibble: 3 × 5
  term               estimate std.error statistic   p.value
  <chr>                 <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)          0.0160   0.00364      4.40 0.0000111
2 democracyDemocracy  -0.0139   0.00398     -3.50 0.000475 
3 ethfrac              0.0186   0.00651      2.86 0.00425

What is predicted probability of civil war onset for a country that is a democracy and has an ethfrac score of 0.5?

prob = 0.016 + (1*-0.014) + 0.5*0.019
prob
[1] 0.0115

  • Save model as an object

  • Remove the tidy() so it is saved as a model object

mod <- linear_reg() %>%
  set_engine("lm") %>%
  fit(ucdponset ~ democracy + ethfrac, data = conflictData)

  • Create new data frame for prediction
predData <- data.frame(democracy = "Democracy", ethfrac = .5)
predData
  democracy ethfrac
1 Democracy     0.5

  • Use predict() to generate predicted values
predict(mod, predData)
# A tibble: 1 × 1
   .pred
   <dbl>
1 0.0114

  • For a non-democracy, how does the predicted probability of civil war onset change if ethfrac changed from 0.25 to 0.75?

predData2 <- data.frame(democracy = c("Autocracy", "Autocracy"), 
                       ethfrac = c(.25, .75))
predData2
  democracy ethfrac
1 Autocracy    0.25
2 Autocracy    0.75

predict(mod, predData2)
# A tibble: 2 × 1
   .pred
   <dbl>
1 0.0207
2 0.0300

Plot Predicted Values from Model

predData3 <- data.frame(democracy = c("Autocracy", "Autocracy", "Autocracy", "Autocracy",
                        "Democracy", "Democracy", "Democracy", "Democracy"), 
                       ethfrac = c(.2, .4, .6,  .8,
                                    .2, .4, .6, .8)
                       )
predData3
  democracy ethfrac
1 Autocracy     0.2
2 Autocracy     0.4
3 Autocracy     0.6
4 Autocracy     0.8
5 Democracy     0.2
6 Democracy     0.4
7 Democracy     0.6
8 Democracy     0.8

Plot Predicted Values from Model

probs <- predict(mod, predData3)
plotData <- cbind(predData3, probs)
plotData
  democracy ethfrac       .pred
1 Autocracy     0.2 0.019751861
2 Autocracy     0.4 0.023477869
3 Autocracy     0.6 0.027203877
4 Autocracy     0.8 0.030929885
5 Democracy     0.2 0.005843543
6 Democracy     0.4 0.009569551
7 Democracy     0.6 0.013295559
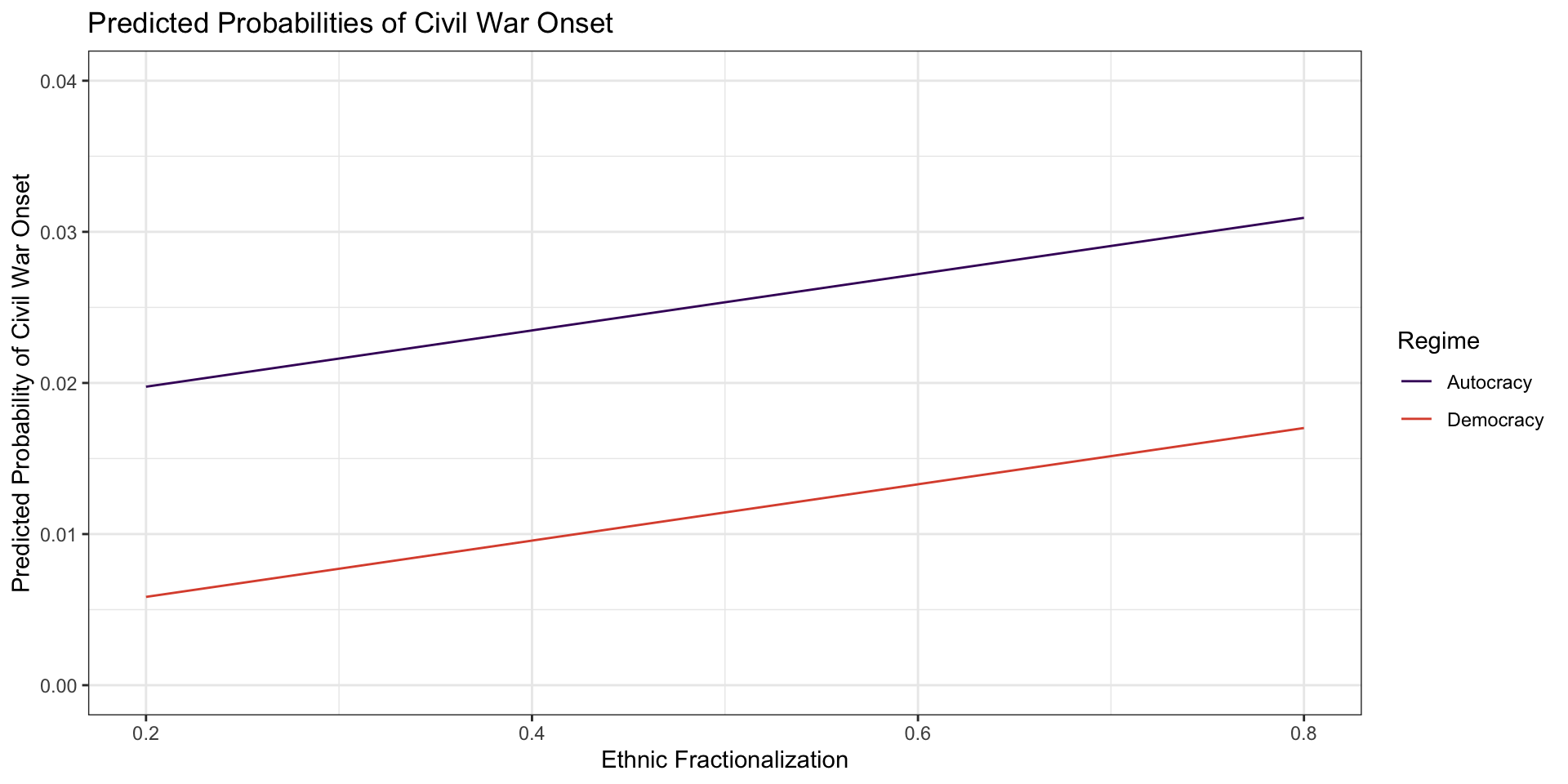
8 Democracy     0.8 0.017021567

Plot Predicted Values from Model

Code 
ggplot(plotData, aes(x = ethfrac, y = .pred, color = democracy)) +
  geom_line() + theme_bw() + labs(x = "Ethnic Fractionalization", 
  y = "Predicted Probability of Civil War Onset", color = "Regime",
  title = "Predicted Probabilities of Civil War Onset") + scale_color_viridis_d(option = "B", begin = .2, end = .6) + ylim(0, 0.04)

IAFF 6501 Website