Interaction Models

January 29, 2025

Load packages

library(tidyverse)
library(dplyr)
library(ggplot2)
library(tidymodels)
library(patchwork)
library(DT)
library(vdemdata)

Multiple Predictors: Interaction Models

Example: Oil Wealth and Democracy

What is the political resource curse?

Set up data: Use the year 2005

oilData <- vdem %>% 
  filter(year == 2005) %>% 
  select(country_name, v2x_libdem, e_gdppc, v2cacamps, e_total_oil_income_pc, v2x_corr, v2pepwrgen, v2clgencl) %>% 
  mutate(lg_gdppc = log(e_gdppc))

Distribution of Oil Wealth per Capita

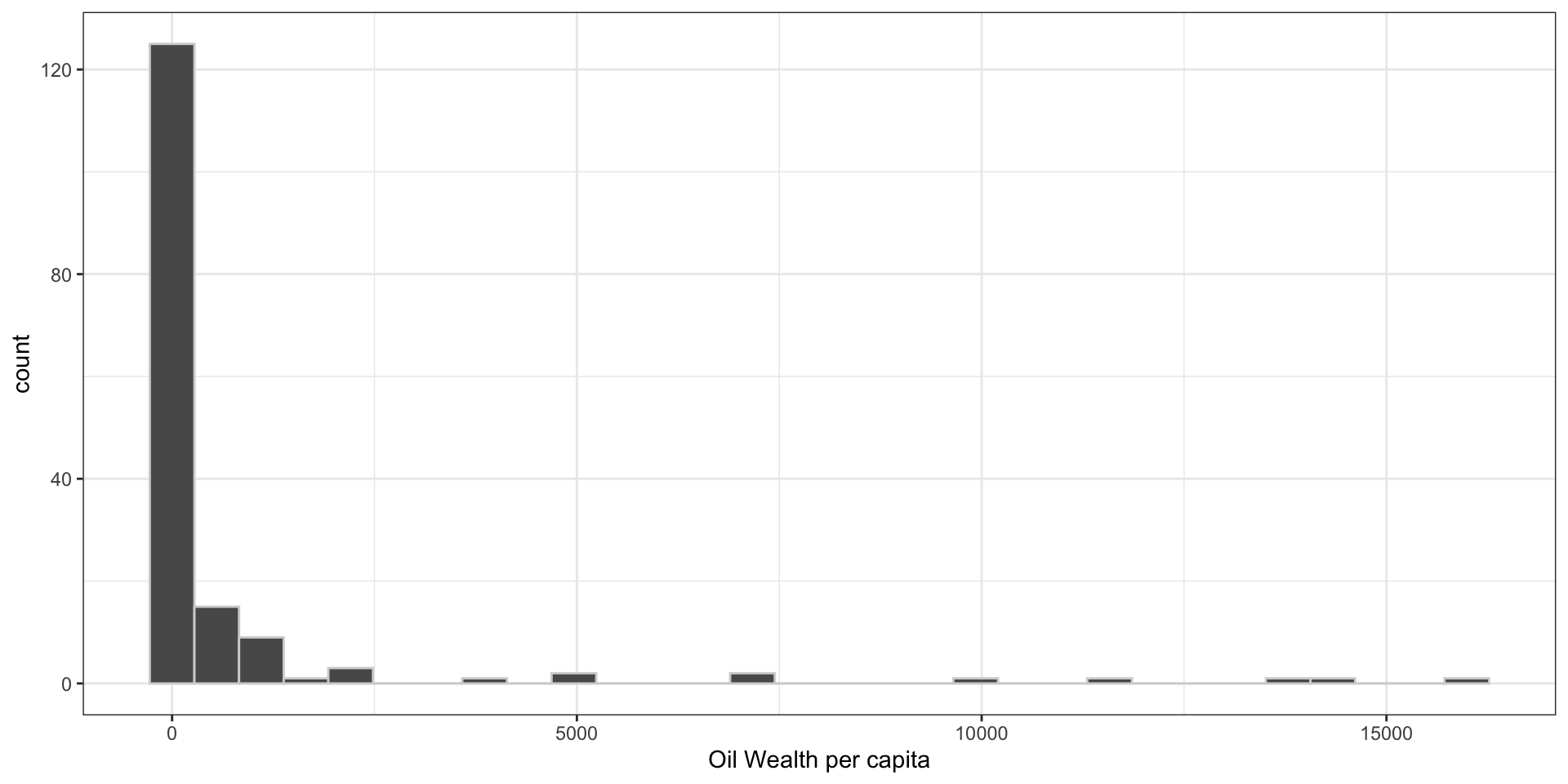
Create a Dummy Variable for High Oil Wealth

oilData <- oilData %>% 
  mutate(
        oil = ifelse(e_total_oil_income_pc > 152, 1, 0),
         oil = factor(oil, labels=c("No Oil Wealth", "Oil Wealth"))
        ) %>% 
  filter(oil == "No Oil Wealth" | oil == "Oil Wealth")
table(oilData$oil)


No Oil Wealth    Oil Wealth 
          122            41

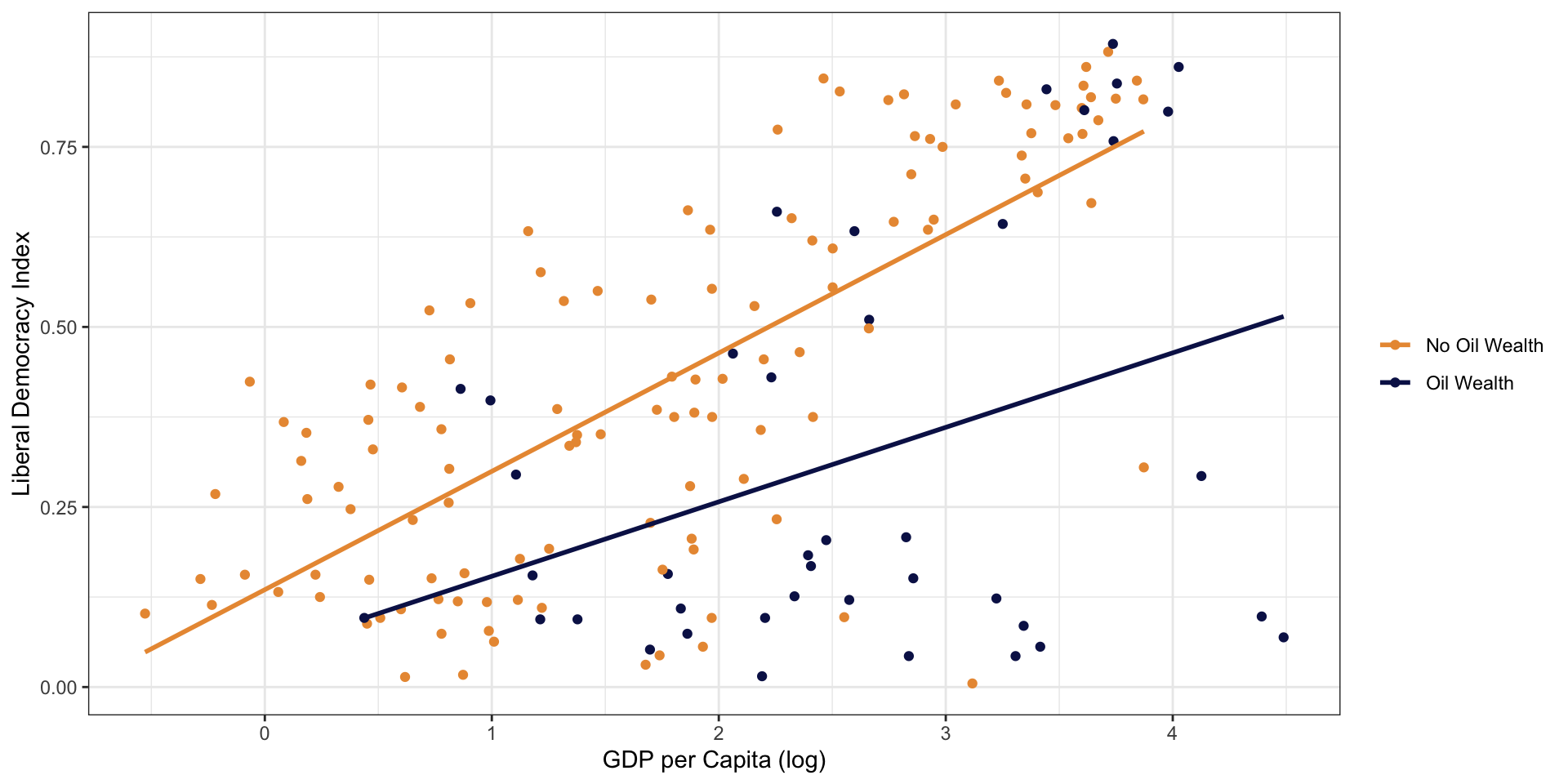
Democracy, GDP, and Oil

How should we interpret this graph?

Model with Oil and GDP per Capita, No Interaction

What is correct interpretation of these results?

linear_reg() %>%
  set_engine("lm") %>%
  fit(v2x_libdem ~ lg_gdppc + oil, data = oilData) %>% 
  tidy()

# A tibble: 3 × 5
  term          estimate std.error statistic  p.value
  <chr>            <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)      0.157    0.0318      4.95 1.84e- 6
2 lg_gdppc         0.152    0.0143     10.6  3.25e-20
3 oilOil Wealth   -0.234    0.0394     -5.93 1.85e- 8

Interaction Model

Question: Does GDP per capita have a different relationship to democracy in Oil rich versus non-Oil rich countries?

Interaction Model

\(Y_i = a + b_1*GDPpc + b_2*Oil + b_3*GDPpc*Oil\)

\(b_3*GDPpc*OilWealth\) captures the interaction

Interaction Model: Interpretation

How should we interpret \(a\)?

\(Y_i = a + b_1*GDPpc + b_2*Oil + b_3*GDPpc*Oil\)

\(a\) is predicted level of democracy where GDPpc = 0 and Oil Wealth = 0

Interaction Model: Interpretation

What happens if we set Oil Wealth to 0?
\(Y_i = a + b_1 * GDPpc + b_2 * Oil + b_3 * GDPpc * Oil\)
\(Y_i = a + b_1 * GDPpc + b_2 * 0 + b_3 * GDPpc * 0\)
\(Y_i = a + b_1 * GDPpc\)

\(b_1\) is the association between GDP per capita and democracy, when oil wealth = 0

Interaction Model: Interpretation

What happens if we set GDPpc to 0?
\(Y_i = a + b_1 * GDPpc + b_2 * Oil + b_3 * GDPpc * Oil\)
\(Y_i = a + b_1 * 0 + b_2 * Oil + b_3 * Oil * 0\)
\(Y_i = a + b_2 * Oil\)
\(b_2\) is the association between oil and democracy, when GDP per capita = 0

Interaction Model: Interpretation

What happens if we set Oil Wealth to 1?

\(Y_i = a + b_1 * GDPpc + b_2 * 1 + b_3 * GDPpc * 1\)

\(Y_i = a + b_1 * GDPpc + b_2 + b_3 * GDPpc\)

Rearrange: \(Y_i = a + (b_1 + b_3) * GDPpc + b_2\)

Interaction Model: Interpretation

\(Y_i = a + (b_1 + b_3) * GDPpc + b_2\)

\(b_1 + b_3\) is the association between GDP per capita and democracy, when oil wealth = 1
\(b_3\) is the difference in the association between GDP per capita and democracy for high oil wealth versus low oil wealth countries.

Run the Interaction Model

linear_reg() %>%
  set_engine("lm") %>%
  fit(v2x_libdem ~ lg_gdppc*oil, data = oilData) %>% 
  tidy()

# A tibble: 4 × 5
  term                   estimate std.error statistic  p.value
  <chr>                     <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)              0.135     0.0341     3.97  1.10e- 4
2 lg_gdppc                 0.164     0.0160    10.3   2.33e-19
3 oilOil Wealth           -0.0848    0.0949    -0.894 3.73e- 1
4 lg_gdppc:oilOil Wealth  -0.0609    0.0354    -1.72  8.70e- 2

Interpretation

\(\hat{Y_i}\) = .138 + .164 * \(GDPpc_i\) + (-0.085) * \(Oil_i\) + (-0.0607) * \(GDPpc_i\) * \(Oil_i\)

Relationship between GDP and democracy without oil: \(0.164\)

Relationship with oil: \(0.164 -0.0607 = 0.1033\)

Conclusion?

Wealth predicts greater democracy, but to a lesser degree when that wealth is driven by oil wealth

Is this difference due to chance?

Does GDP have a lower relationship to democracy in oil rich countries?
Is 0.164 without oil different from 0.1033 with oil?

What is the null hypothesis? What is the alternative?

Is this difference due to chance?

We can interpret the p-value in the same way as we learned previously. Same with the 95 percent confidence intervals.

# A tibble: 4 × 6
  term                   estimate std.error p.value conf.low conf.high
  <chr>                     <dbl>     <dbl>   <dbl>    <dbl>     <dbl>
1 (Intercept)               0.135     0.034   0        0.068     0.202
2 lg_gdppc                  0.164     0.016   0        0.133     0.196
3 oilOil Wealth            -0.085     0.095   0.373   -0.272     0.103
4 lg_gdppc:oilOil Wealth   -0.061     0.035   0.087   -0.131     0.009

Is this difference due to chance?

95% Confidence Interval: [-0.131, 0.009]: mostly negative
p-value of interaction term: 0.089
- this is higher that 0.05, but close and remember that the cutoff is arbitrary

Questions?

Another Example: Resume Experiement

Is gender discrimination in call backs different for those with or without a college degree?

Fit interaction model

library(openintro)
linear_reg() %>%
  set_engine("lm") %>%
  fit(received_callback ~ gender*college_degree, data = resume) %>% 
  tidy()

# A tibble: 4 × 5
  term                   estimate std.error statistic  p.value
  <chr>                     <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)             0.0796    0.00775    10.3   1.71e-24
2 genderm                 0.0463    0.0247      1.88  6.04e- 2
3 college_degree          0.00429   0.00946     0.453 6.51e- 1
4 genderm:college_degree -0.0635    0.0267     -2.38  1.74e- 2

# A tibble: 4 × 5
  term                   estimate std.error statistic  p.value
  <chr>                     <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)             0.0796    0.00775    10.3   1.71e-24
2 genderm                 0.0463    0.0247      1.88  6.04e- 2
3 college_degree          0.00429   0.00946     0.453 6.51e- 1
4 genderm:college_degree -0.0635    0.0267     -2.38  1.74e- 2

\(\hat{Y_i}\) = .08 + .05 * \(M_i\) + 0.004 * \(Coll_i\) + (-0.06) * \(M_i\) * \(Coll_i\)