Logistic Regression

Classification

May 19, 2025

Review

Review

  • True or False: When the coefficient on a predictor is statistically significant, we have proved that the predictor has a causal impact on the outcome?
  • False: The answer depends on the research design.

Review

  • True or False: When the coefficient on a predictor is statistically significant, we have proved that the predictor has large and important association with outcome?
  • False: The answer depends on your substantive interpretation of the effect sizes and on your knowledge of the specific issue.

Models with Binary (0/1) Outcomes

Binary Outcomes

  • So far we have looked at continuous or numerical outcomes (response variables)

  • We are often also interested in outcome variables that are binary (Yes/No, or 0/1)

    • Did violence happen, or not?
    • Classification: is this email spam?

Racial Discrimination Study

Bertrand and Mullainathan (2003)

data are in openintro package

glimpse(resume)
Rows: 4,870
Columns: 30
$ job_ad_id              <dbl> 384, 384, 384, 384, 385, 386, 386, 385, 386, 38…
$ job_city               <chr> "Chicago", "Chicago", "Chicago", "Chicago", "Ch…
$ job_industry           <chr> "manufacturing", "manufacturing", "manufacturin…
$ job_type               <chr> "supervisor", "supervisor", "supervisor", "supe…
$ job_fed_contractor     <dbl> NA, NA, NA, NA, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, N…
$ job_equal_opp_employer <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ job_ownership          <chr> "unknown", "unknown", "unknown", "unknown", "no…
$ job_req_any            <dbl> 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0,…
$ job_req_communication  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0,…
$ job_req_education      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ job_req_min_experience <chr> "5", "5", "5", "5", "some", "", "", "some", "",…
$ job_req_computer       <dbl> 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0,…
$ job_req_organization   <dbl> 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0,…
$ job_req_school         <chr> "none_listed", "none_listed", "none_listed", "n…
$ received_callback      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ firstname              <chr> "Allison", "Kristen", "Lakisha", "Latonya", "Ca…
$ race                   <chr> "white", "white", "black", "black", "white", "w…
$ gender                 <chr> "f", "f", "f", "f", "f", "m", "f", "f", "f", "m…
$ years_college          <int> 4, 3, 4, 3, 3, 4, 4, 3, 4, 4, 4, 4, 4, 4, 4, 1,…
$ college_degree         <dbl> 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0,…
$ honors                 <int> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ worked_during_school   <int> 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0,…
$ years_experience       <int> 6, 6, 6, 6, 22, 6, 5, 21, 3, 6, 8, 8, 4, 4, 5, …
$ computer_skills        <int> 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1,…
$ special_skills         <int> 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1,…
$ volunteer              <int> 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0,…
$ military               <int> 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ employment_holes       <int> 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0,…
$ has_email_address      <int> 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0,…
$ resume_quality         <chr> "low", "high", "low", "high", "high", "low", "h…

Racial Discrimination Study

  • Outcome variable: Applicant received call back (yes=1, No=0)

  • Predictors:

    • Race of applicant (randomly assigned)
    • Years of Experience

Racial Discrimination Study

# A tibble: 2 × 2
  race  callRate
  <chr>    <dbl>
1 black   0.0645
2 white   0.0965

Racial Discrimination Study

Racial Discrimination Study

Racial Discrimination Study

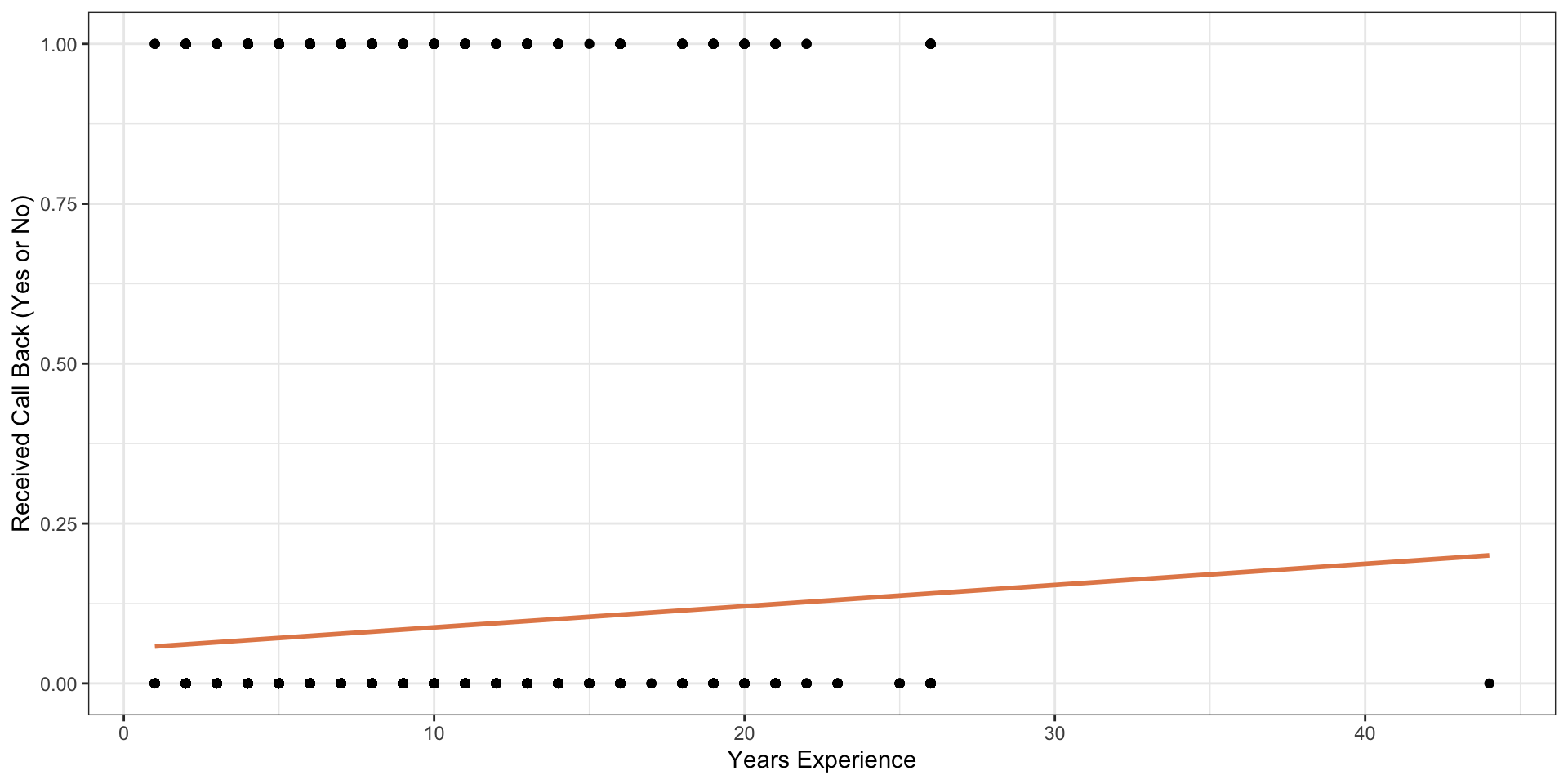
We want a model to predict call backs: our linear models do not really work in this situation

Modeling

  • We can treat each outcome (call back or not) as successes and failures arising from separate Bernoulli trials

    • Bernoulli trial: a random experiment with exactly two possible outcomes, “success” and “failure”, in which the probability of success is the same every time the experiment is conducted

Modeling

  • Each Bernoulli trial can have a separate probability of success

yi∼Bern(p)

Modeling

  • We can then use the predictor variables to model that probability of success, pi

  • We can’t use a linear model for pi (since pi must be between 0 and 1) but we can transform the linear model to have the appropriate range

Generalized linear models

  • This is a very general way of addressing many problems in regression and the resulting models are called generalized linear models (GLMs)

  • Logistic regression is a very common example

GLMs

All GLMs have the following three characteristics:

  • A probability distribution describing a generative model for the outcome variable
  • A linear model: η=β0+β1X1+⋯+βkXk
  • A link function that relates the linear model to the parameter of the outcome distribution

Logistic regression

  • Logistic regression is a GLM used to model a binary categorical outcome (0 or 1)

  • In logistic regression, the link function that connects ηi to pi is the logit function

  • Logit function: For 0≤p≤1

logit(p)=log(p1−p)

Logit function

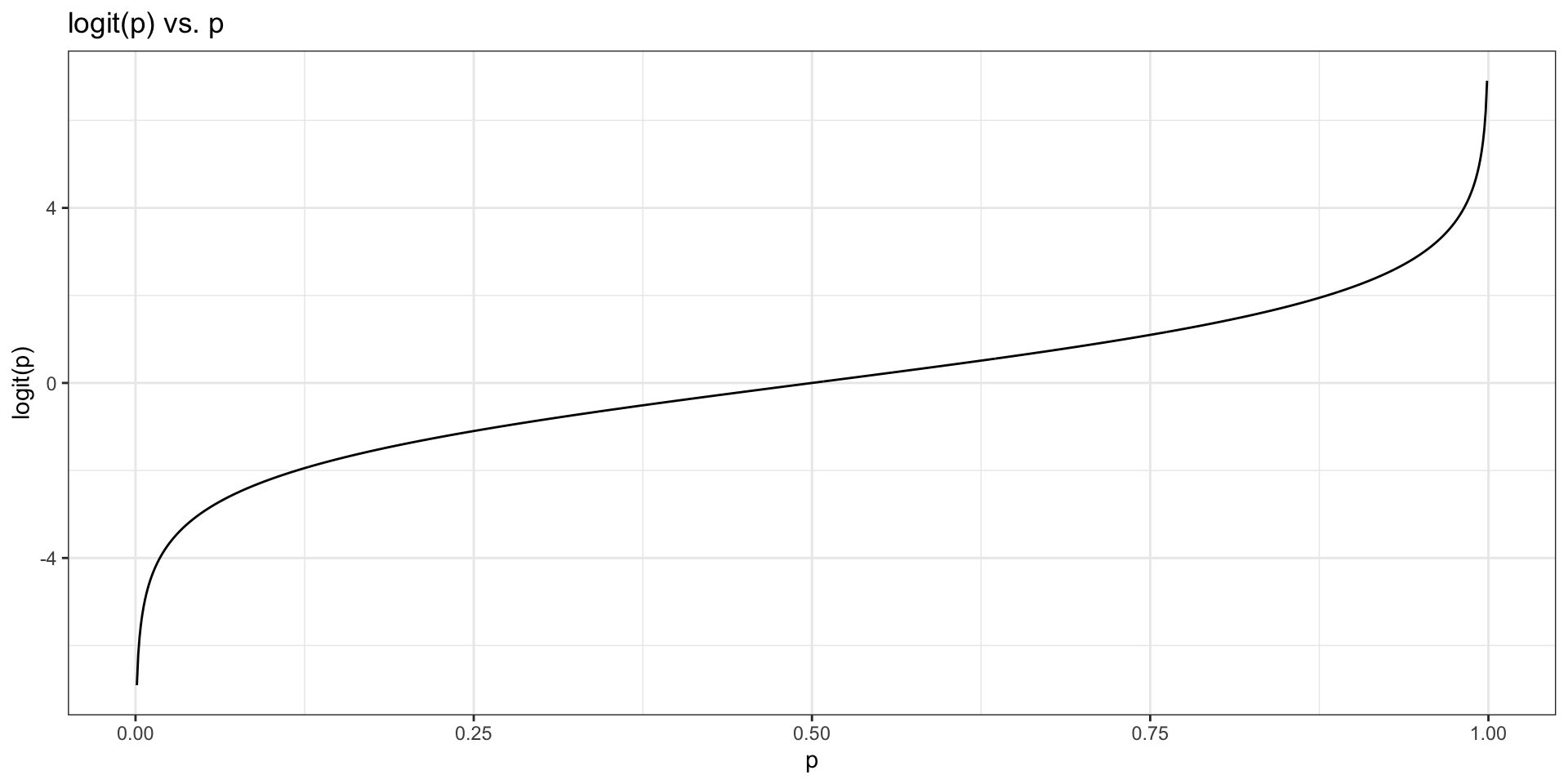
Logit function

  • The logit function takes a value between 0 and 1 and maps it to a value between −∞ and ∞

  • Inverse logit (logistic) function:

g−1(x)=exp(x)1+exp(x)=11+exp(−x)

  • The inverse logit function takes a value between −∞ and ∞ and maps it to a value between 0 and 1

Logistic regression model

  • yi∼Bern(pi)
  • ηi=β0+β1x1,i+⋯+βnxn,i
  • logit(pi)=ηi

Logistic regression model

  • logit(pi)=ηi=β0+β1x1,i+⋯+βnxn,i

  • Now take inverse logit to get p

  • pi=exp(β0+β1x1,i+⋯+βkxk,i)1+exp(β0+β1x1,i+⋯+βkxk,i)

Running logistic regression

  • Implementation is not very difficult now that we know how to run a linear model

  • We just need to update our code to run a GLM

    • specify the model with logistic_reg()
    • use "glm" instead of "lm" as the engine
    • define family = "binomial" for the link function to be used in the model

Running logistic regression

discrim_fit <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(factor(received_callback) ~ years_experience, data = resume, family = "binomial")
tidy(discrim_fit)
# A tibble: 2 × 5
  term             estimate std.error statistic   p.value
  <chr>               <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)       -2.76     0.0962     -28.7  5.58e-181
2 years_experience   0.0391   0.00918      4.26 2.07e-  5

Interpretation

  • The results here are for the linear model predicting ηi

  • This makes them hard to interpret

  • We need to convert into predicted probabilities

    • We can use the inverse logit function to do this

Interpretation

  • The intercept is -2.76

  • When all predictors at 0, ηi=−2.76

  • Logistic function: exp(ηi)(1+exp(ηi))


exp(-2.76) / (1 + exp(-2.76))
[1] 0.05952437

Predicted Probabilities

newdata <- tibble(
  years_experience = c(0, 5, 15, 25)
  )

Predicted Probabilities

y_hat <- predict(discrim_fit, newdata, type = "raw")

# Use inverse logit function to get predicted probabilities
p_hat <- exp(y_hat) / (1 + exp(y_hat))

# merge to our new data
newdata <- newdata %>%
  bind_cols(
    y_hat = y_hat,
    p_hat = p_hat
  )
newdata
# A tibble: 4 × 3
  years_experience y_hat  p_hat
             <dbl> <dbl>  <dbl>
1                0 -2.76 0.0595
2                5 -2.56 0.0715
3               15 -2.17 0.102 
4               25 -1.78 0.144

Predicted Probabilities

expand for full code 
ggplot(newdata, aes(y=p_hat, x = years_experience)) +
  geom_point(color = "#0C1956") +
  geom_line(color = "#0C1956") +
  scale_x_continuous(breaks=seq(0, 30, 5)) +
  scale_y_continuous(breaks=seq(0, .75, .05)) +
  ylim(0, .25) +
  labs(
    x = "Years Experience",
    y = "Predicted Probability of Call Back", 
    title = ""
  ) +
  theme_bw()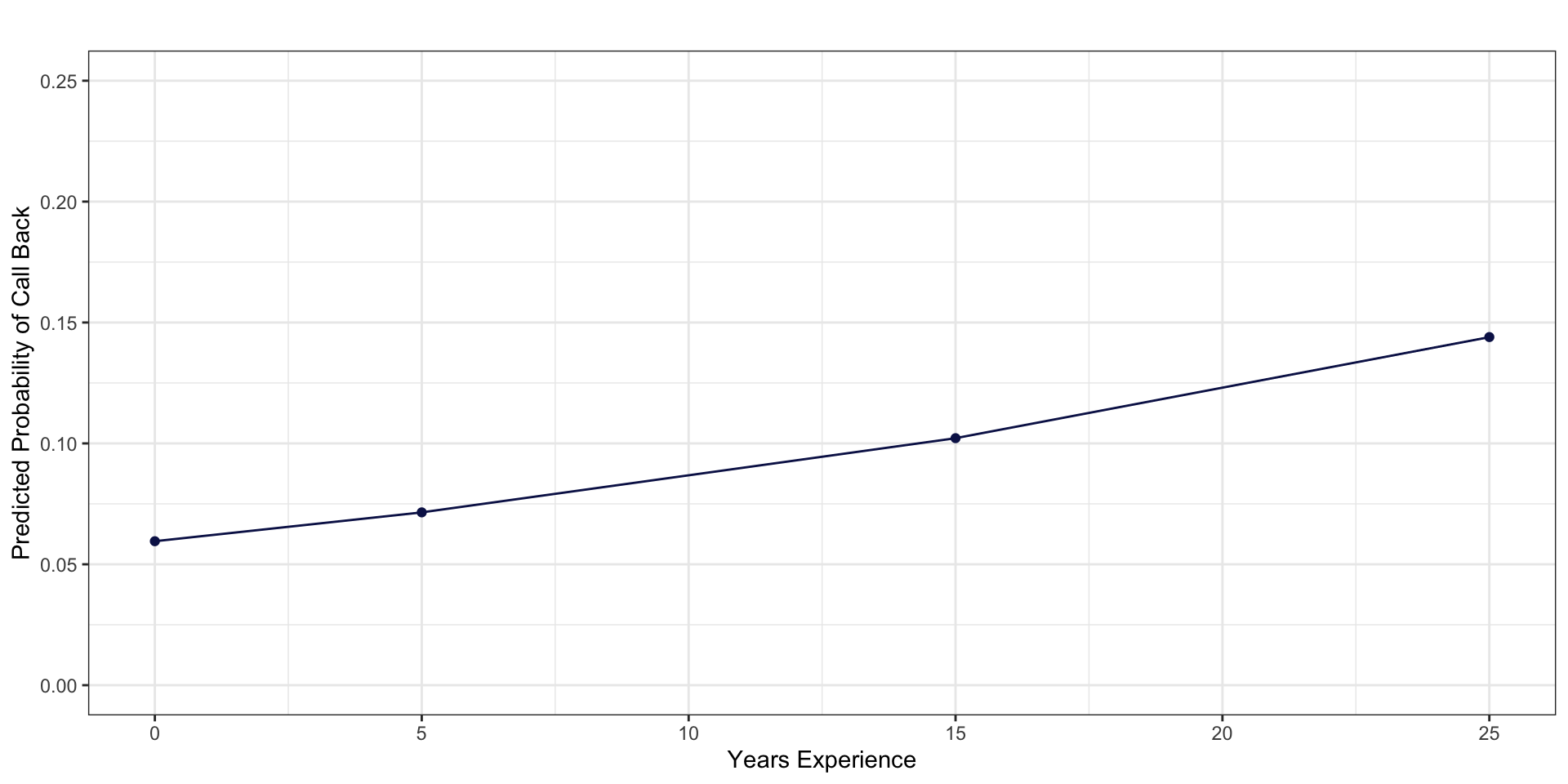

Racial Discrimination Model

discrim_fit <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(factor(received_callback) ~ race, data = resume, family = "binomial")
tidy(discrim_fit)
# A tibble: 2 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)   -2.67     0.0825    -32.4  1.59e-230
2 racewhite      0.438    0.107       4.08 4.45e-  5

Predicted Probabilities

newdata <- tibble(
  race = c("white", "black")
  )

Predicted Probabilities

y_hat <- predict(discrim_fit, newdata, type = "raw")

# Take inverse logit of y_hat to get predicted probabilities
p_hat <- exp(y_hat) / (1 + exp(y_hat))

# merge to our new data
newdata <- newdata %>%
  bind_cols(
    y_hat = y_hat,
    p_hat = p_hat
  )
newdata
# A tibble: 2 × 3
  race  y_hat  p_hat
  <chr> <dbl>  <dbl>
1 white -2.24 0.0965
2 black -2.67 0.0645

Is this difference due to chance?

tidy(discrim_fit, conf.int=TRUE)
# A tibble: 2 × 7
  term        estimate std.error statistic   p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)   -2.67     0.0825    -32.4  1.59e-230   -2.84     -2.52 
2 racewhite      0.438    0.107       4.08 4.45e-  5    0.229     0.650

Is this difference due to chance?

Very unlikely to be due to chance

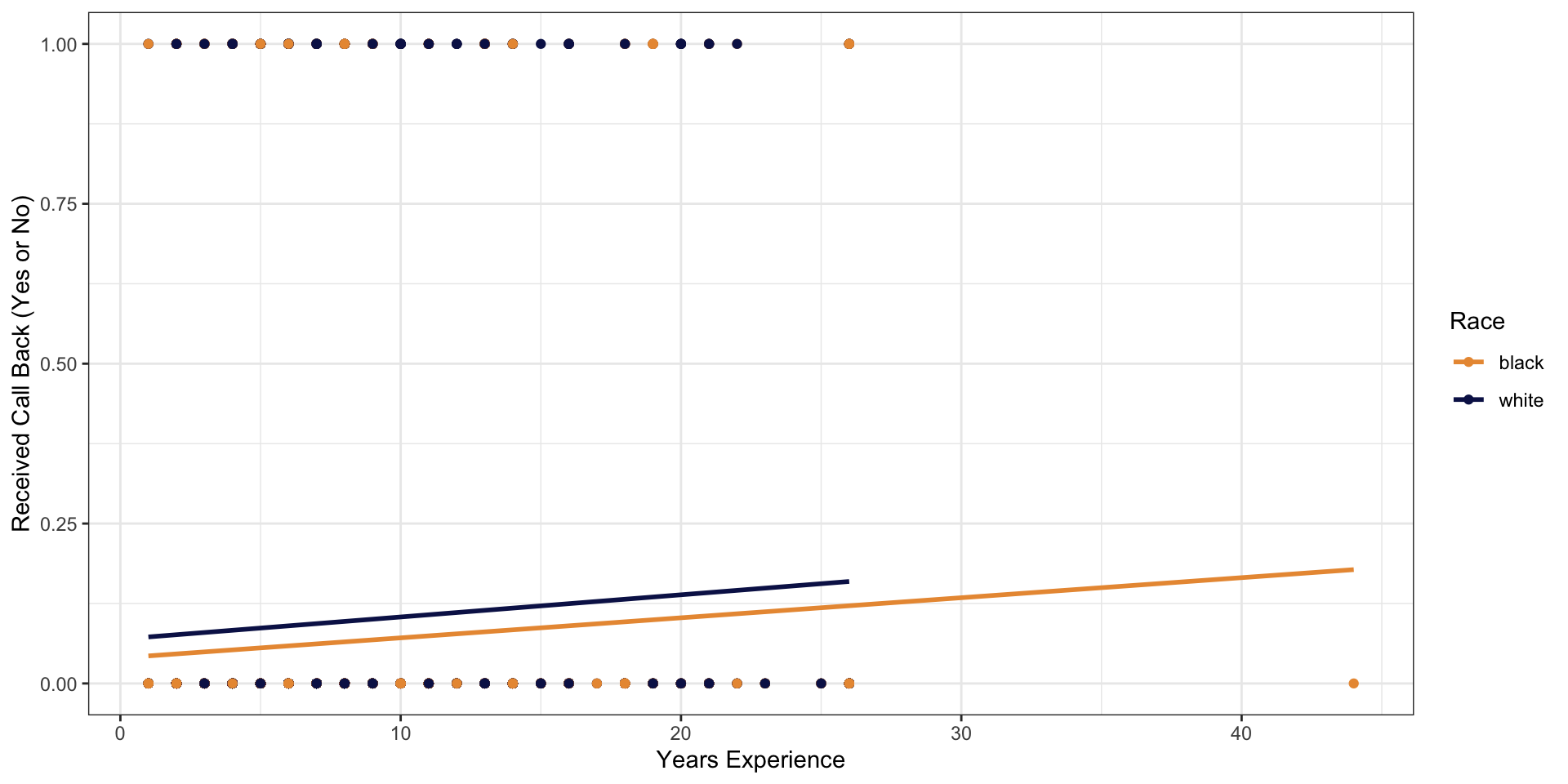
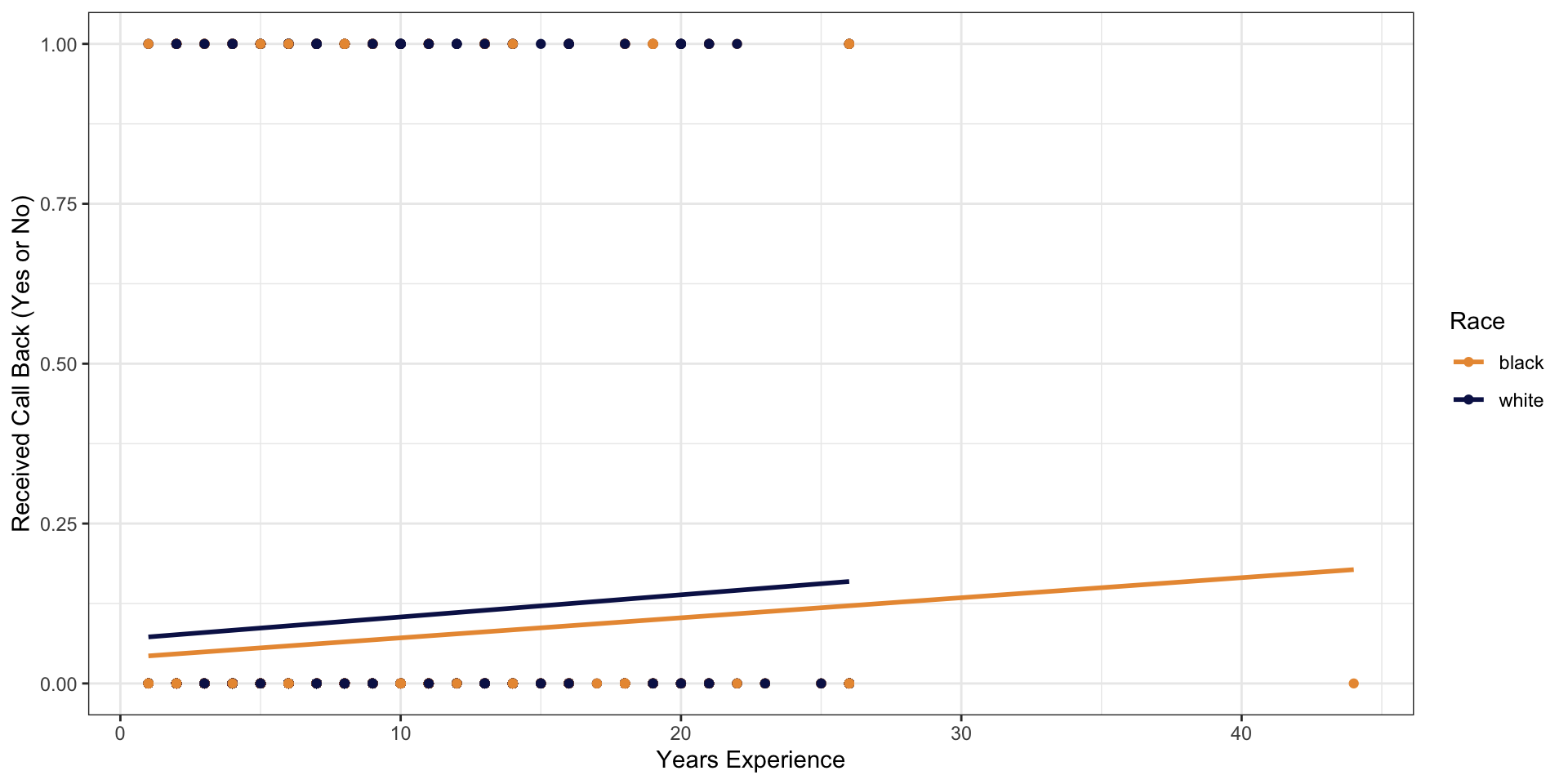
Multiple Predictors

discrim_fit <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(factor(received_callback) ~ race + years_experience, data = resume, family = "binomial")
tidy(discrim_fit)
# A tibble: 3 × 5
  term             estimate std.error statistic   p.value
  <chr>               <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)       -3.00     0.116      -25.9  2.37e-148
2 racewhite          0.438    0.108        4.08 4.56e-  5
3 years_experience   0.0391   0.00920      4.25 2.14e-  5

Predicted Probabilities

# variable names need to be same as in dataset
newdata <- tibble(
  race = c("white", "black", "white", "black", "white", "black", "white", "black"),
  years_experience = c(0, 0, 10, 10, 20, 20, 30, 30)
  )
newdata
# A tibble: 8 × 2
  race  years_experience
  <chr>            <dbl>
1 white                0
2 black                0
3 white               10
4 black               10
5 white               20
6 black               20
7 white               30
8 black               30

Predicted Probabilities

y_hat <- predict(discrim_fit, newdata, type = "raw")
p_hat <- exp(y_hat) / (1 + exp(y_hat))
# merge to our new data
newdata <- newdata %>%
  bind_cols(
    y_hat = y_hat,
    p_hat = p_hat
  )
newdata
# A tibble: 8 × 4
  race  years_experience y_hat  p_hat
  <chr>            <dbl> <dbl>  <dbl>
1 white                0 -2.56 0.0717
2 black                0 -3.00 0.0475
3 white               10 -2.17 0.103 
4 black               10 -2.61 0.0686
5 white               20 -1.78 0.144 
6 black               20 -2.22 0.0982
7 white               30 -1.39 0.200 
8 black               30 -1.83 0.139

Plotting Predicted Probabilities

expand for full code 
newdata %>% 
  ggplot(., aes(y=p_hat, x=years_experience, color=race)) +
  geom_point() +
  geom_line() +
  labs(x = "Years Experience", y = "Predicted Pr(Call Back)")  +
    scale_color_manual(name="Race", 
                      values = c("#E99840", "#0C1956")) +
  theme_bw()

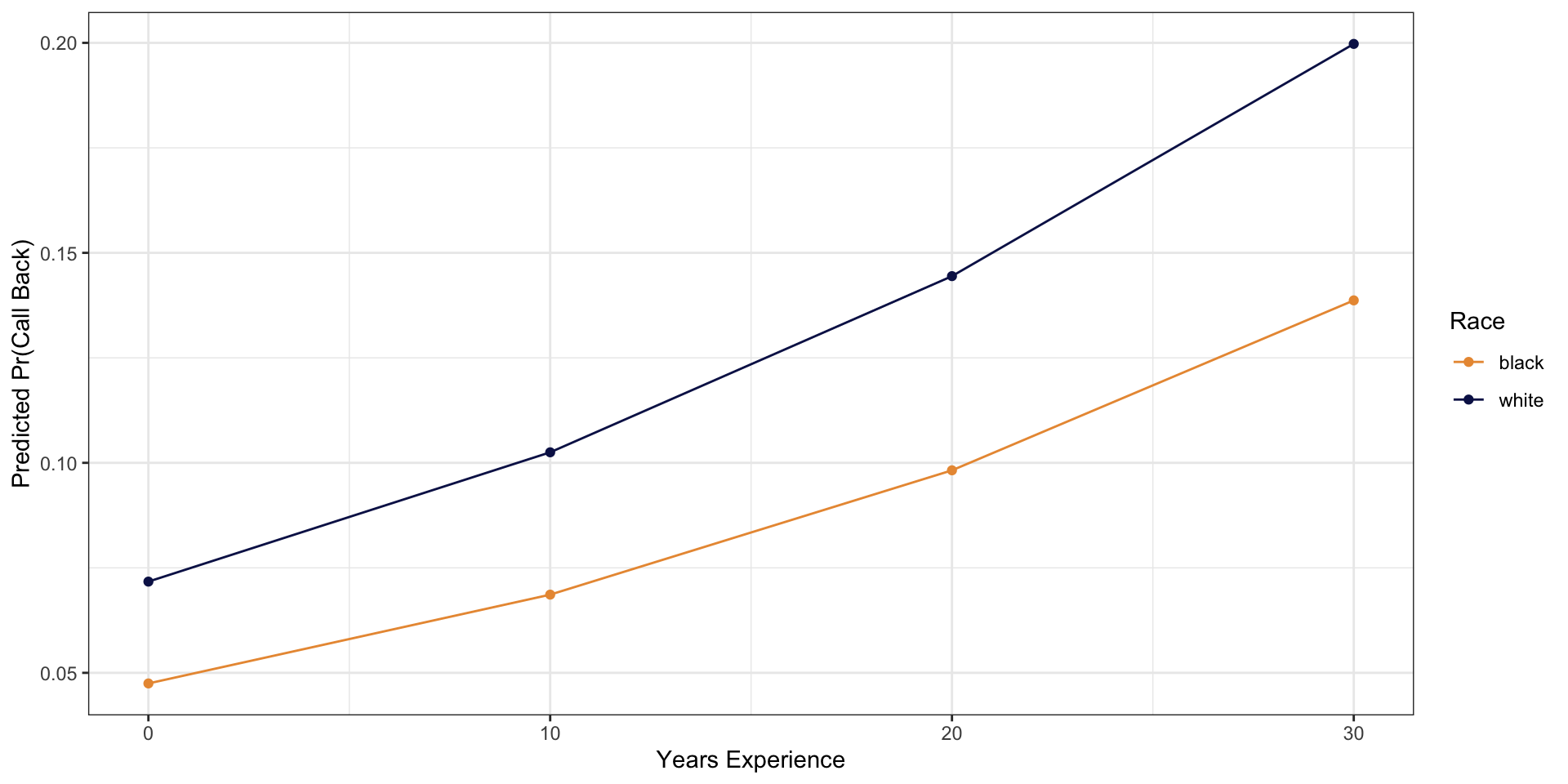
Plotting Predicted Probabilities

  • In a linear model with no interactions, the impact of race would not vary depending on other values of other measures (years_experience).

  • This is not the case for logistic regression because of the transformation.

  • For interpretation, it is important to set the values of the other predictors

Your Turn: Fit and Interpret Logistic Regression

library(openintro)
names(email)
 [1] "spam"         "to_multiple"  "from"         "cc"           "sent_email"  
 [6] "time"         "image"        "attach"       "dollar"       "winner"      
[11] "inherit"      "viagra"       "password"     "num_char"     "line_breaks" 
[16] "format"       "re_subj"      "exclaim_subj" "urgent_subj"  "exclaim_mess"
[21] "number"      
table(email$winner)

  no  yes 
3857   64

Spam Filter: Fit Model

spam_fit <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(factor(spam) ~ winner, data = email, family = "binomial")
tidy(spam_fit)
# A tibble: 2 × 5
  term        estimate std.error statistic      p.value
  <chr>          <dbl>     <dbl>     <dbl>        <dbl>
1 (Intercept)    -2.31    0.0563    -41.1  0           
2 winneryes       1.53    0.275       5.54 0.0000000306

Spam Filter: Data for prediction

newdata <- newdata <- tibble(
  winner = c("no", "yes")
  )
newdata
# A tibble: 2 × 1
  winner
  <chr> 
1 no    
2 yes

Spam Filter: Predicted Probabilities

y_hat <- predict(spam_fit, newdata, type = "raw")
p_hat <- exp(y_hat) / (1 + exp(y_hat))
# merge to our new data
newdata <- newdata %>%
  bind_cols(
    y_hat = y_hat,
    p_hat = p_hat
  )
newdata
# A tibble: 2 × 3
  winner  y_hat  p_hat
  <chr>   <dbl>  <dbl>
1 no     -2.31  0.0900
2 yes    -0.788 0.312

Try a different variable

library(openintro)
library(tidymodels)
library(tidyverse)
names(email)
 [1] "spam"         "to_multiple"  "from"         "cc"           "sent_email"  
 [6] "time"         "image"        "attach"       "dollar"       "winner"      
[11] "inherit"      "viagra"       "password"     "num_char"     "line_breaks" 
[16] "format"       "re_subj"      "exclaim_subj" "urgent_subj"  "exclaim_mess"
[21] "number"      
table(email$urgent_subj)

   0    1 
3914    7

  • Use table(email$VARNAME) to determine values of the variable you choose.

  • Run logistic regresson model and generate predicted probabilities of being spam for each value of the variable

  • Run model with two predictors: winner and the variable you choose. Calculate predicted probabilities.

  • Bonus: Run interaction model and calculate predicted probabilities.

IAFF 6501 Website

1 / 44
Logistic Regression Classification May 19, 2025

  1. Slides

  2. Tools

  3. Close
  • Logistic Regression
  • Review
  • Review
  • Review
  • Models with Binary (0/1) Outcomes
  • Binary Outcomes
  • Racial Discrimination Study
  • Racial Discrimination Study
  • Racial Discrimination Study
  • Racial Discrimination Study
  • Racial Discrimination Study
  • Racial Discrimination Study
  • Modeling
  • Modeling
  • Modeling
  • Generalized linear models
  • GLMs
  • Logistic regression
  • Logit function
  • Logit function
  • Logistic regression model
  • Logistic regression model
  • Running logistic regression
  • Running logistic regression
  • Interpretation
  • Interpretation
  • Predicted Probabilities
  • Predicted Probabilities
  • Predicted Probabilities
  • Racial Discrimination Model
  • Predicted Probabilities
  • Predicted Probabilities
  • Is this difference due to chance?
  • Is this difference due to chance?
  • Multiple Predictors
  • Predicted Probabilities
  • Predicted Probabilities
  • Plotting Predicted Probabilities
  • Plotting Predicted Probabilities
  • Your Turn: Fit and Interpret Logistic Regression
  • Spam Filter: Fit Model
  • Spam Filter: Data for prediction
  • Spam Filter: Predicted Probabilities
  • Try a different variable
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help