Describing and Visualizing Variables

January 29, 2025

Outline


  • Describing and visualizing data

  • Practice with description and visualization

  • Next week: deeper dive on coding and other aspects of Data Visulalization

Types of variables

  • Numerical variables

    • Continuous - infinite values
    • Discrete - non-negative whole numbers

  • Categorical

    • Ordinal – if there is a natural ordering
    • World Region is categorical, but NOT ordinal

Start with summarizing a numerical variable

Let’s Use the V-Dem Data Again

Electoral Democracy Measure


  • To what extent is the ideal of electoral democracy in its fullest sense achieved?

  • Measure runs from 0 (lowest) to 1 (highest) [0.5 is a cutoff they use for determining electoral democracy from electoral autocracy]

  • Clarification: The electoral principle of democracy seeks to embody the core value of making rulers responsive to citizens, achieved through electoral competition for the electorate’s approval under circumstances when suffrage is extensive; political and civil society organizations can operate freely; elections are clean and not marred by fraud or systematic irregularities; and elections affect the composition of the chief executive of the country. In between elections, there is freedom of expression and an independent media capable of presenting alternative views on matters of political relevance.

Other High Level V-Dem Democracy Measures

  • Liberal Democracy
  • Egalitarian Democracy
  • Participatory Democracy
  • Deliberative Democracy

Describe and Summarize


How can we use our data to describe or summarize the state of electoral democracy in the year 2022?

Create the data

# Create dataset for year 2022, with country name, year, and electoral dem
library(vdemlite)
vdem2022 <- fetchdem() %>% 
  mutate(region = e_regionpol_6C) %>% 
  mutate(region = case_match(region, 
                        1 ~ "Eastern Europe", 
                        2 ~ "Latin America",  
                        3 ~ "Middle East",   
                        4 ~ "Africa", 
                        5 ~ "The West", 
                        6 ~ "Asia")) %>%
  filter(year == 2022)  %>% 
  select(country_name, year, v2x_polyarchy, region, v2x_regime)

Examine the data

glimpse(vdem2022)
Rows: 179
Columns: 5
$ country_name  <chr> "Mexico", "Suriname", "Sweden", "Switzerland", "Ghana", …
$ year          <dbl> 2022, 2022, 2022, 2022, 2022, 2022, 2022, 2022, 2022, 20…
$ v2x_polyarchy <dbl> 0.571, 0.775, 0.896, 0.897, 0.664, 0.711, 0.817, 0.091, …
$ region        <chr> "Latin America", "Latin America", "The West", "The West"…
$ v2x_regime    <dbl> 2, 2, 3, 3, 2, 2, 3, 0, 1, 2, 1, 0, 2, 2, 2, 3, 3, 1, 1,…

How can we summarize electoral democracy?

  • “Typical” values

  • Shape of the distribution

  • Spread of the distribution

“Typical” Values

We could calculate the mean (mean)

vdem2022 %>% 
  summarize(mean_democracy = mean(v2x_polyarchy))
  mean_democracy
1      0.4977821

“Typical” Values

We could calculate the median (median)

vdem2022 %>% 
  summarize(median_democracy = median(v2x_polyarchy))
  median_democracy
1            0.507

Describe and visualize the distribution

We can describe the shape of the distribution

  • symmetric
  • right-skewed
  • left-skewed
  • unimodal (one peak)
  • bimodal (multiple peaks)

Symmetric distributions

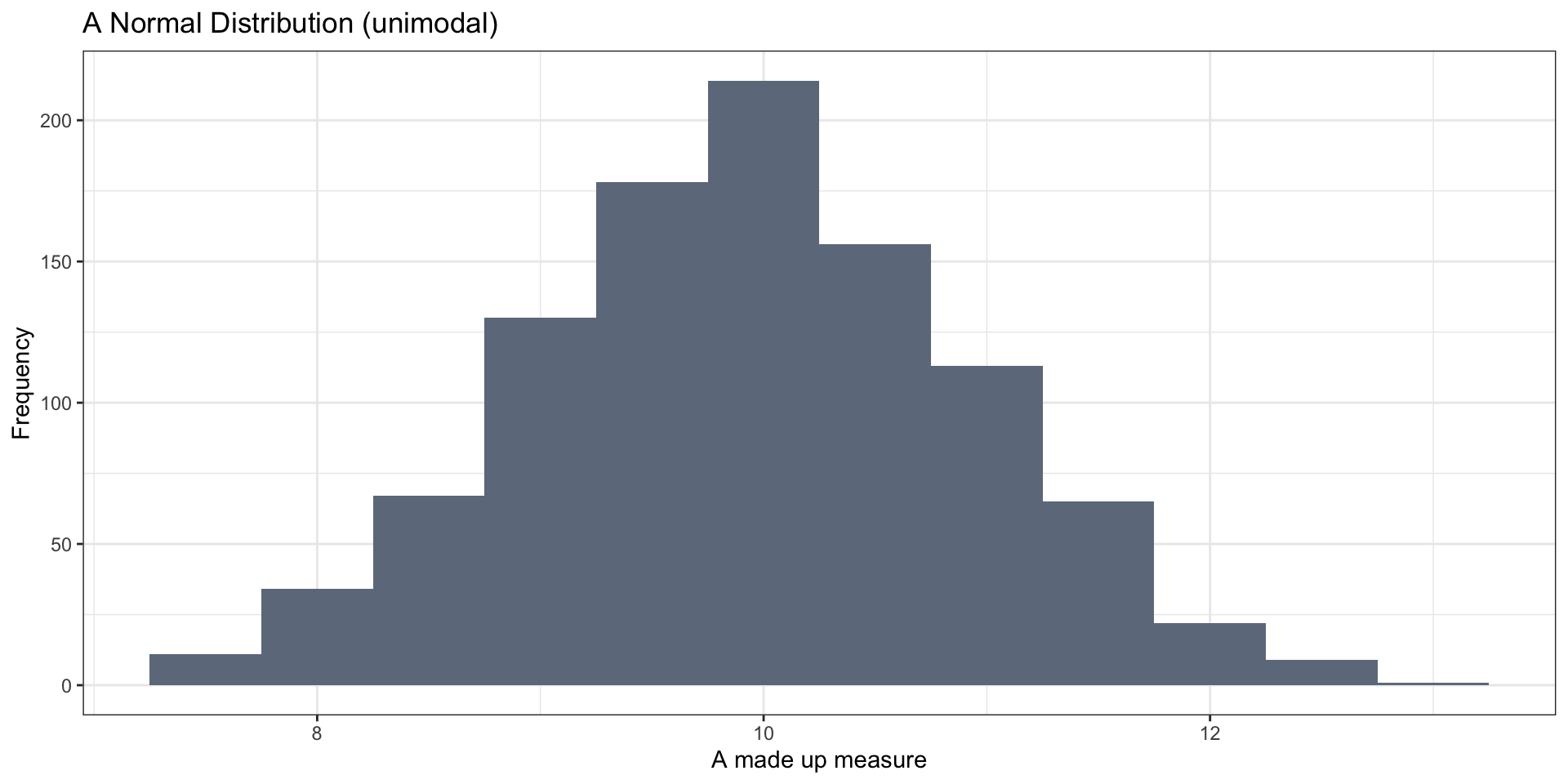
Symmetric distributions

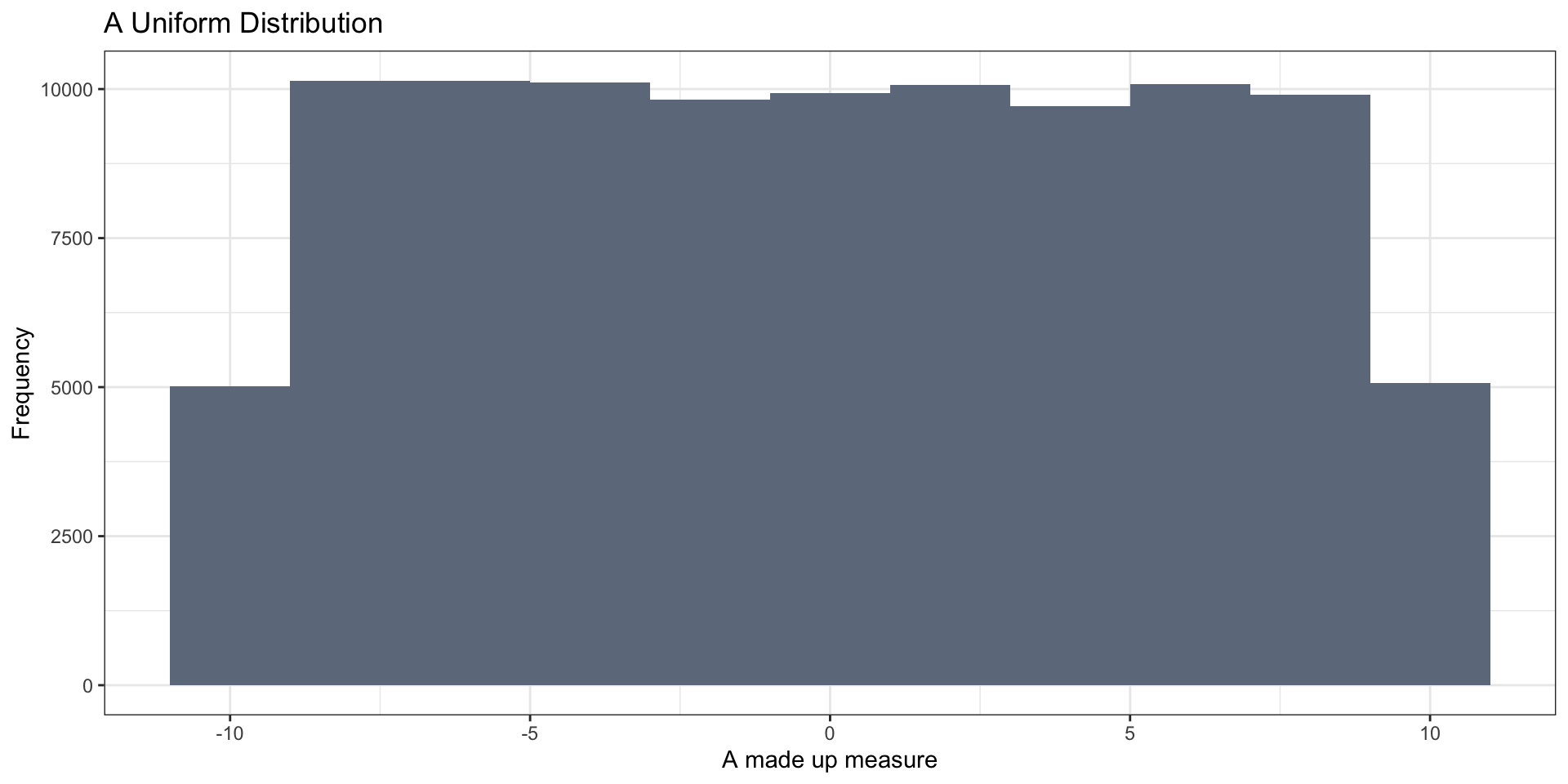
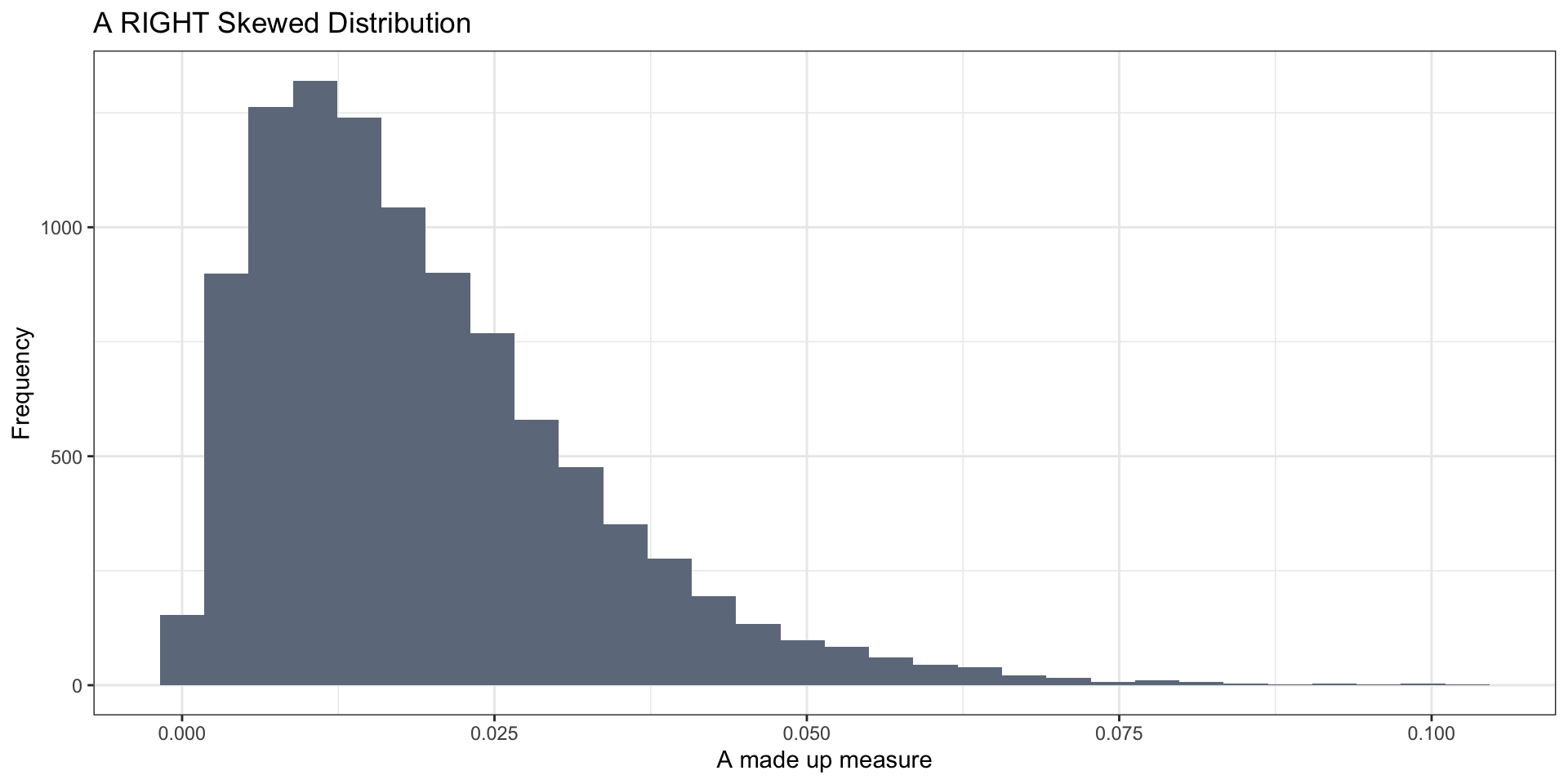
Skewed Distributions

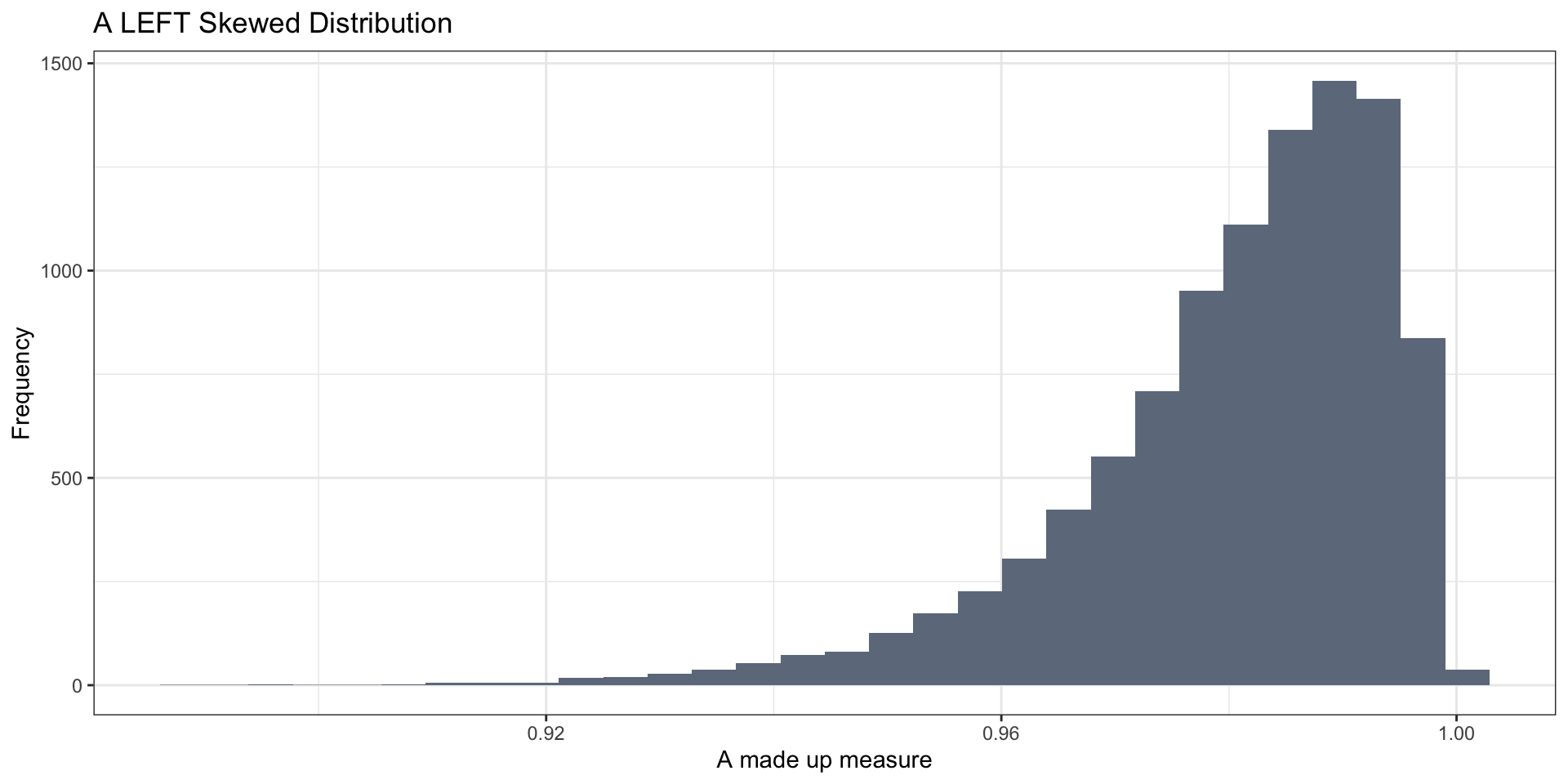
Skewed Distributions

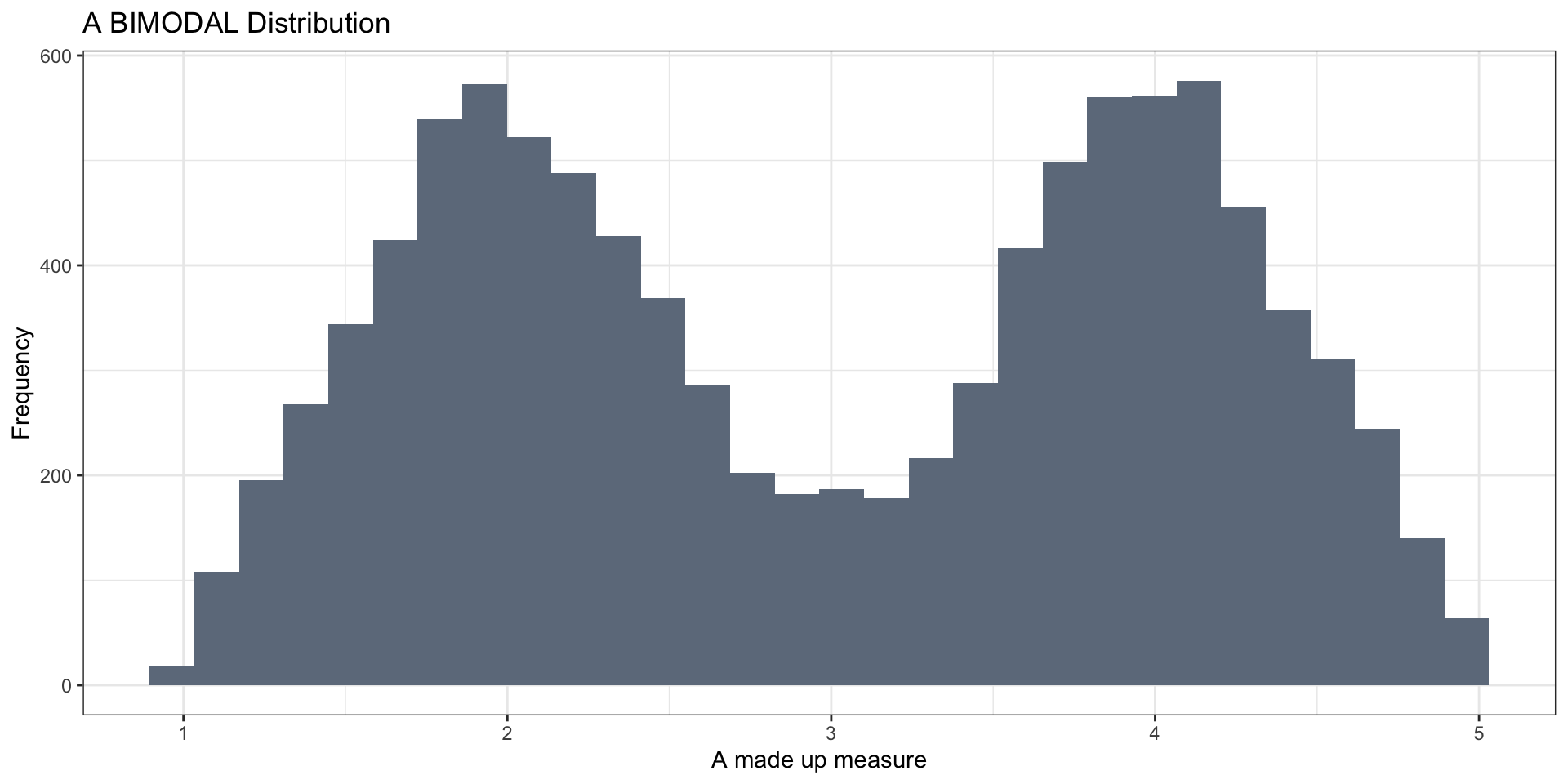
Bimodal Distribution

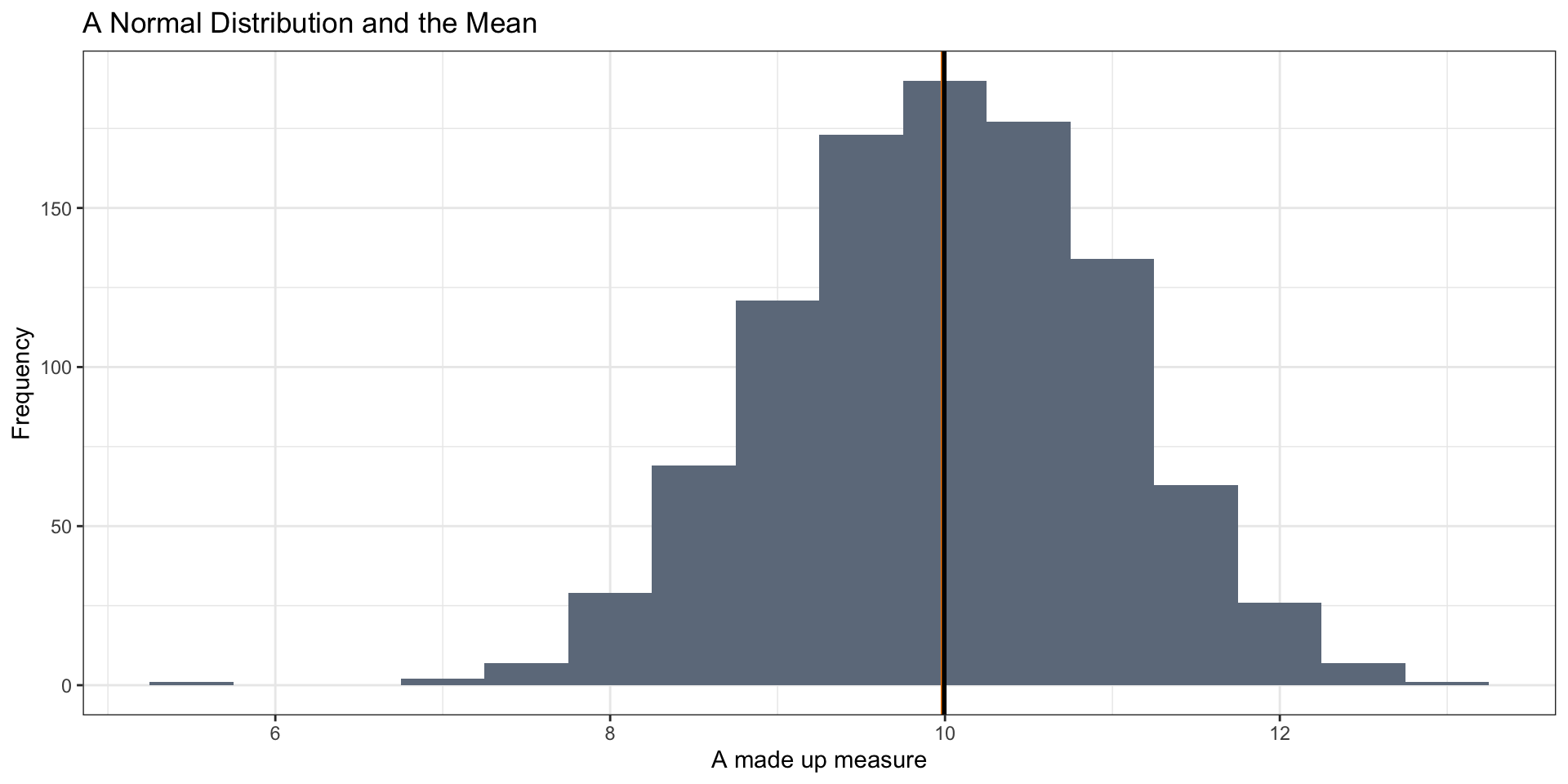
Mean vs Median

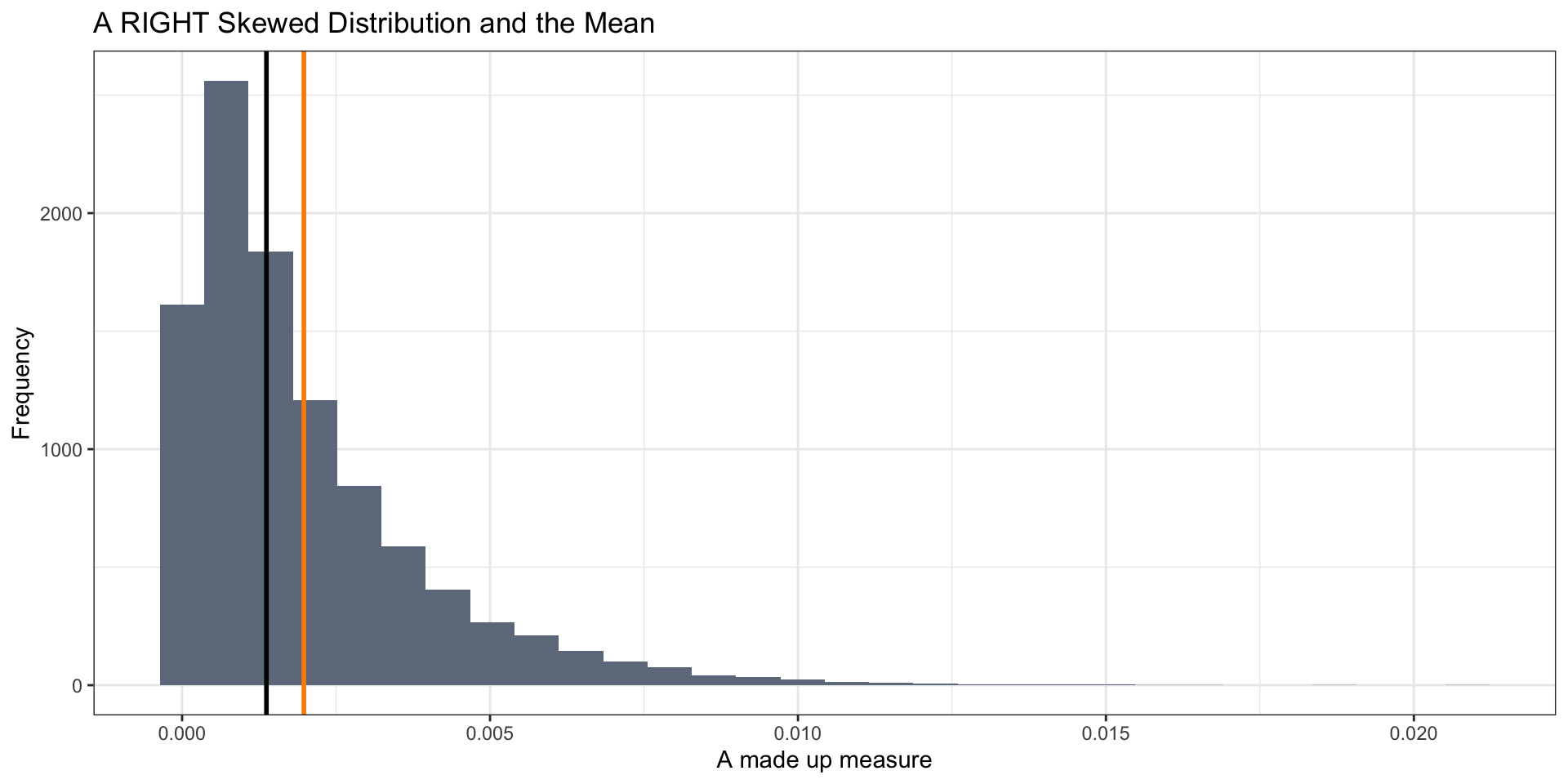
Mean vs Median

Mean vs Median

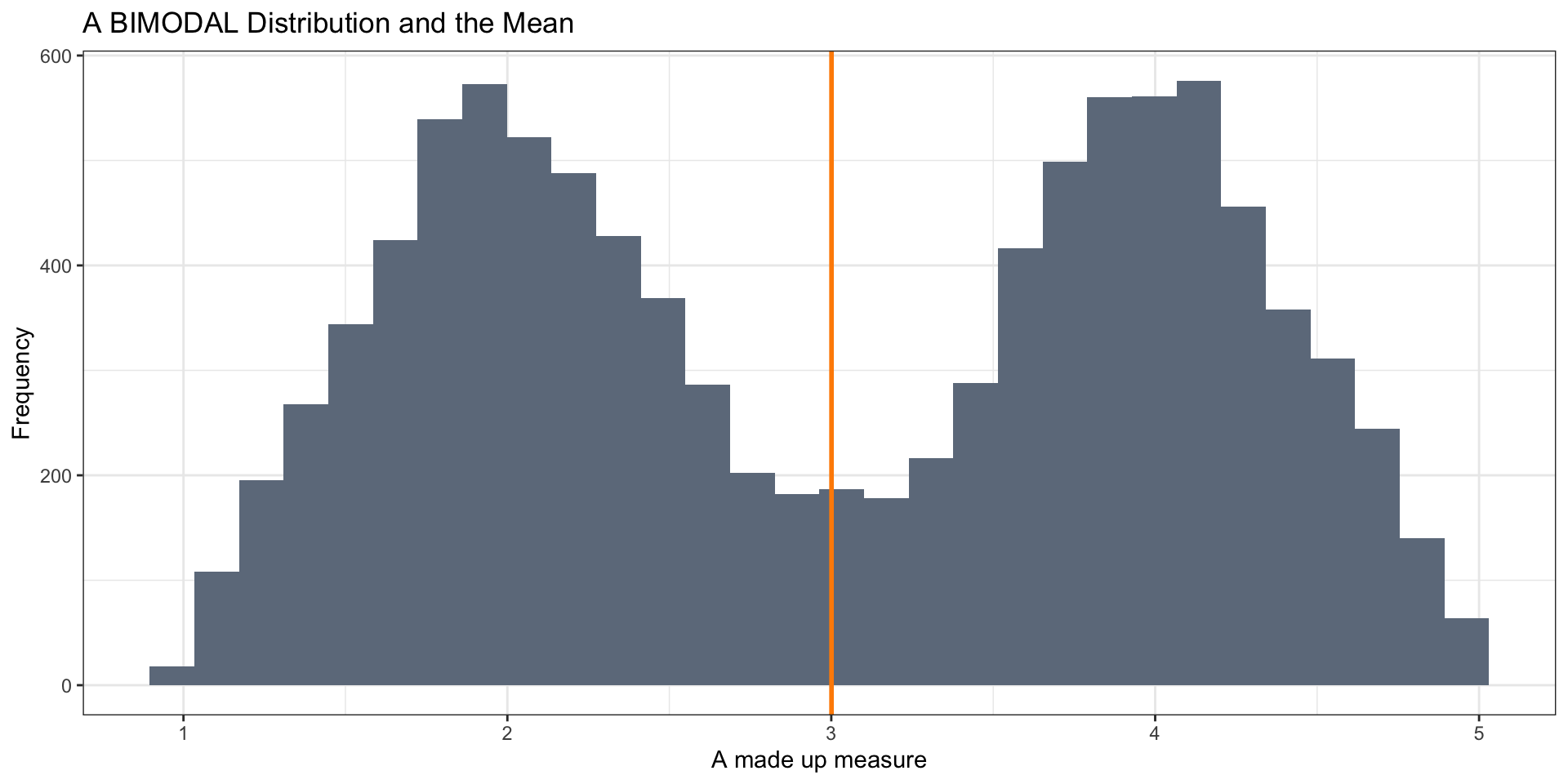
Mean vs Median


  • the Mean works well as a summary statistic when the distribution is relatively symmetric

  • Not as well when distributions are skewed or bimodal (or multi-modal)

    • With skewed distributions, the mean is sensitive to extreme values

  • The median is more robust

Lesson

  • Always look at your data

  • When reading or in a presentation, ask yourself:

    • Does the mean make sense given the distribution of the measure?
    • Could extreme values in a skewed distribution make the mean not as useful?
    • Have the analysts shown you the distribution? If not, ask about it!

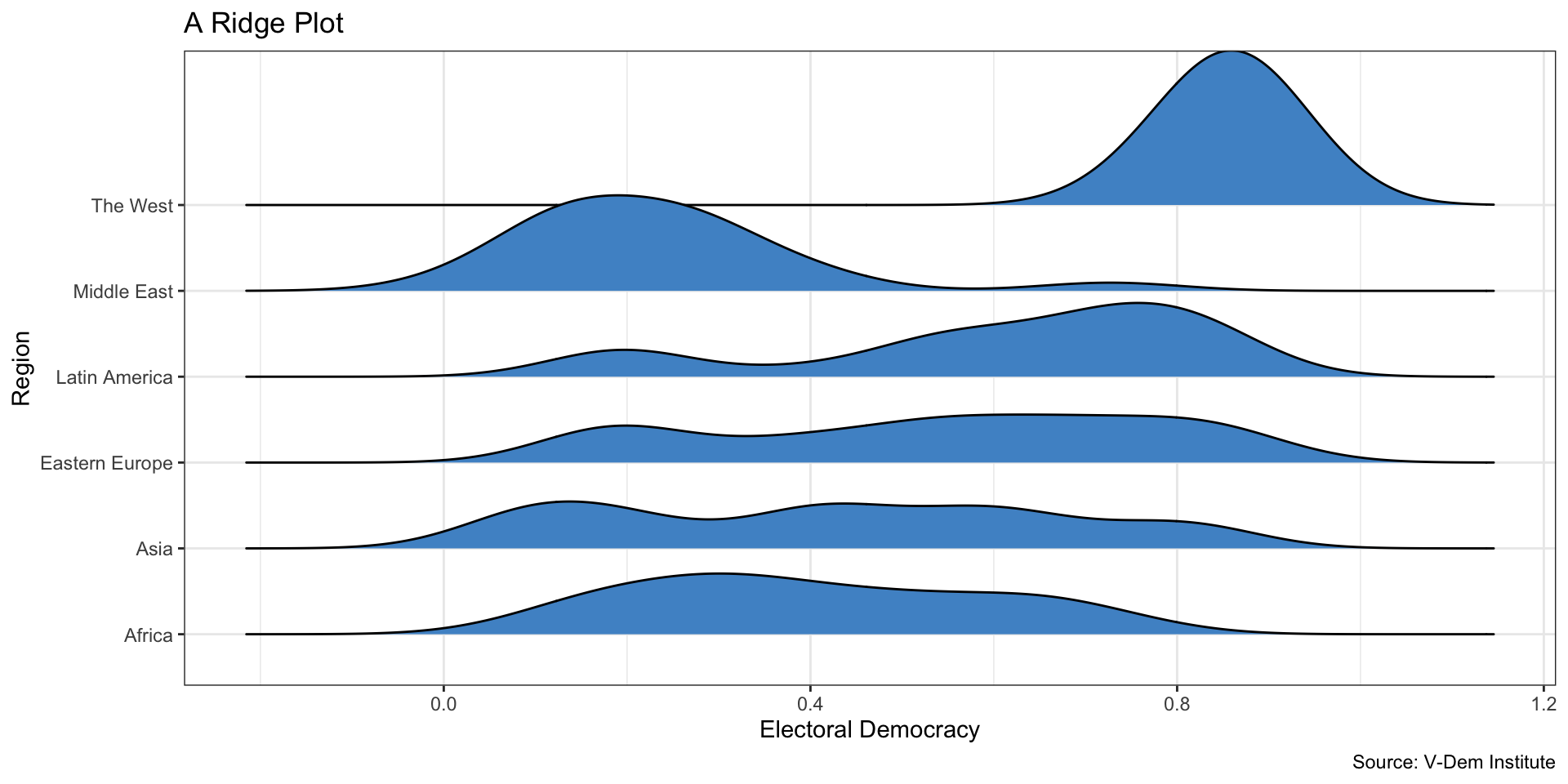
Visualize Our Measure

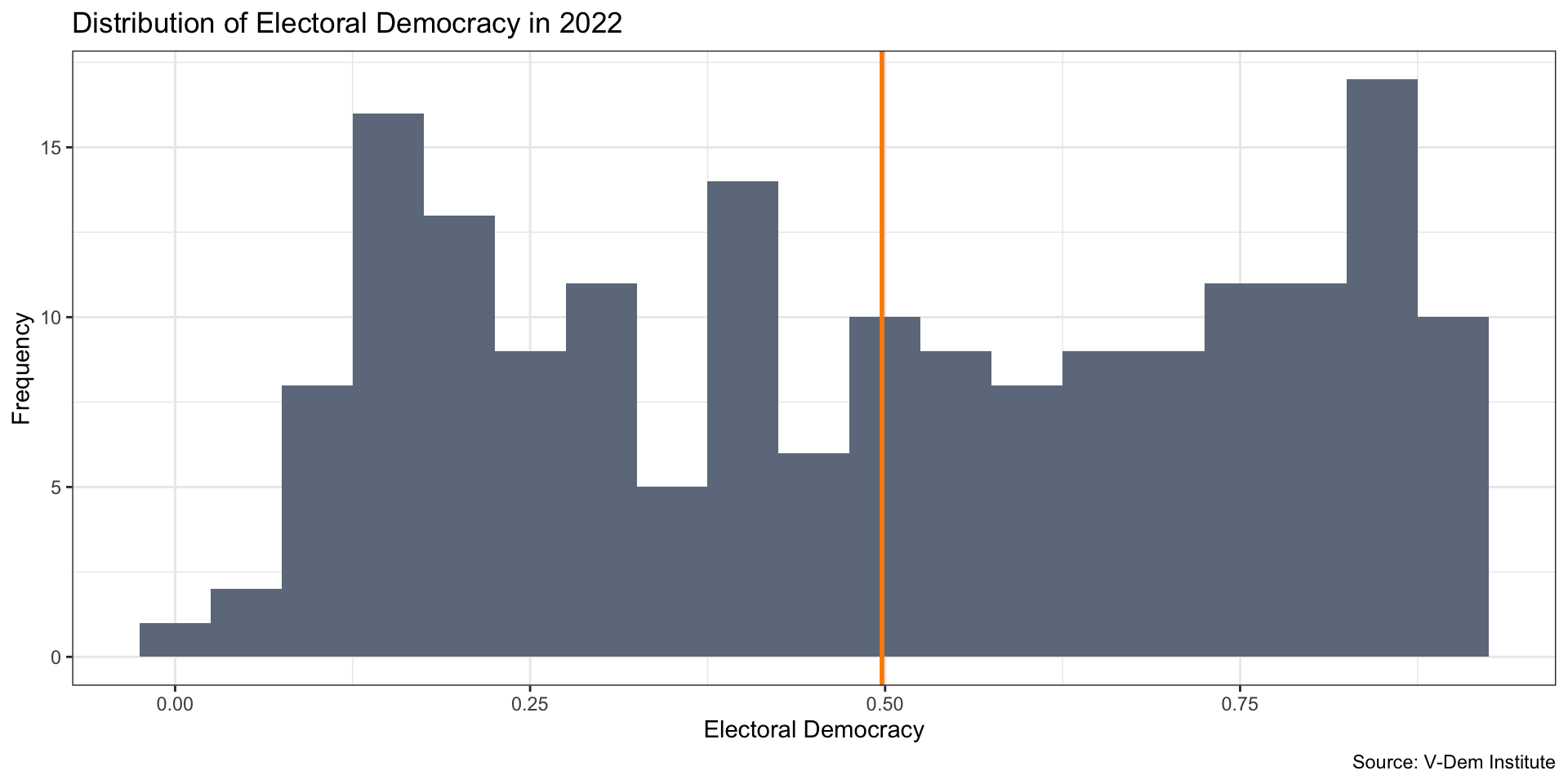
Recap


  • We can use statistics like mean or median to describe the center of a variable

  • We can visualize the entire distribution to characterize the distribution of the variable

  • We should also say something about the spread of the distribution

Why Measure and Visualize Spread?

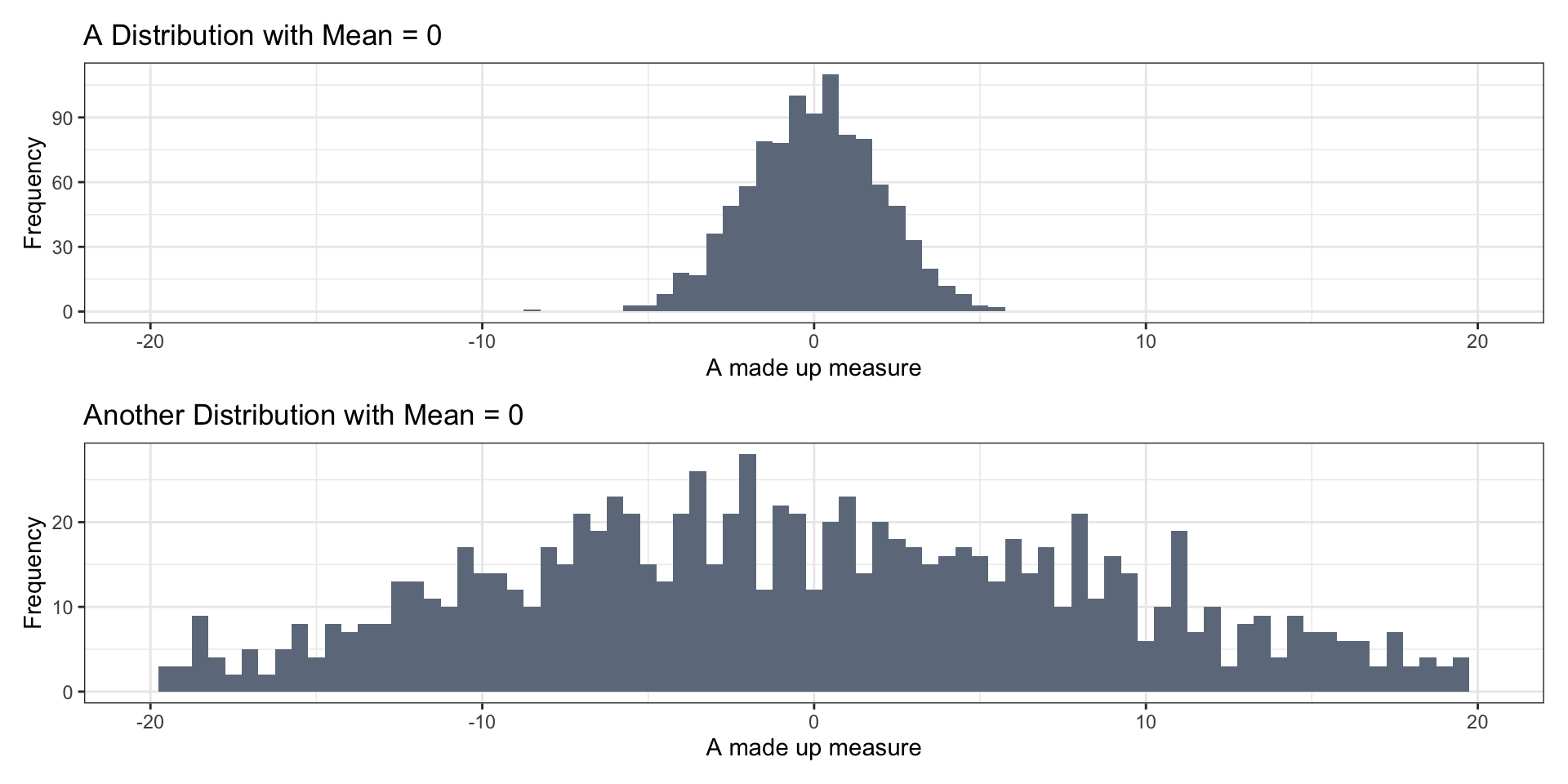
Measures of Spread

  • Range (min and max values)

    • Not ideal b/c does not tell us much about where most of the values are located
vdem2022 %>% 
  summarize(min = min(v2x_polyarchy),
            max = max(v2x_polyarchy))
    min   max
1 0.015 0.915

Interquartile Range

IQR: 25th percentile - 75th percentile

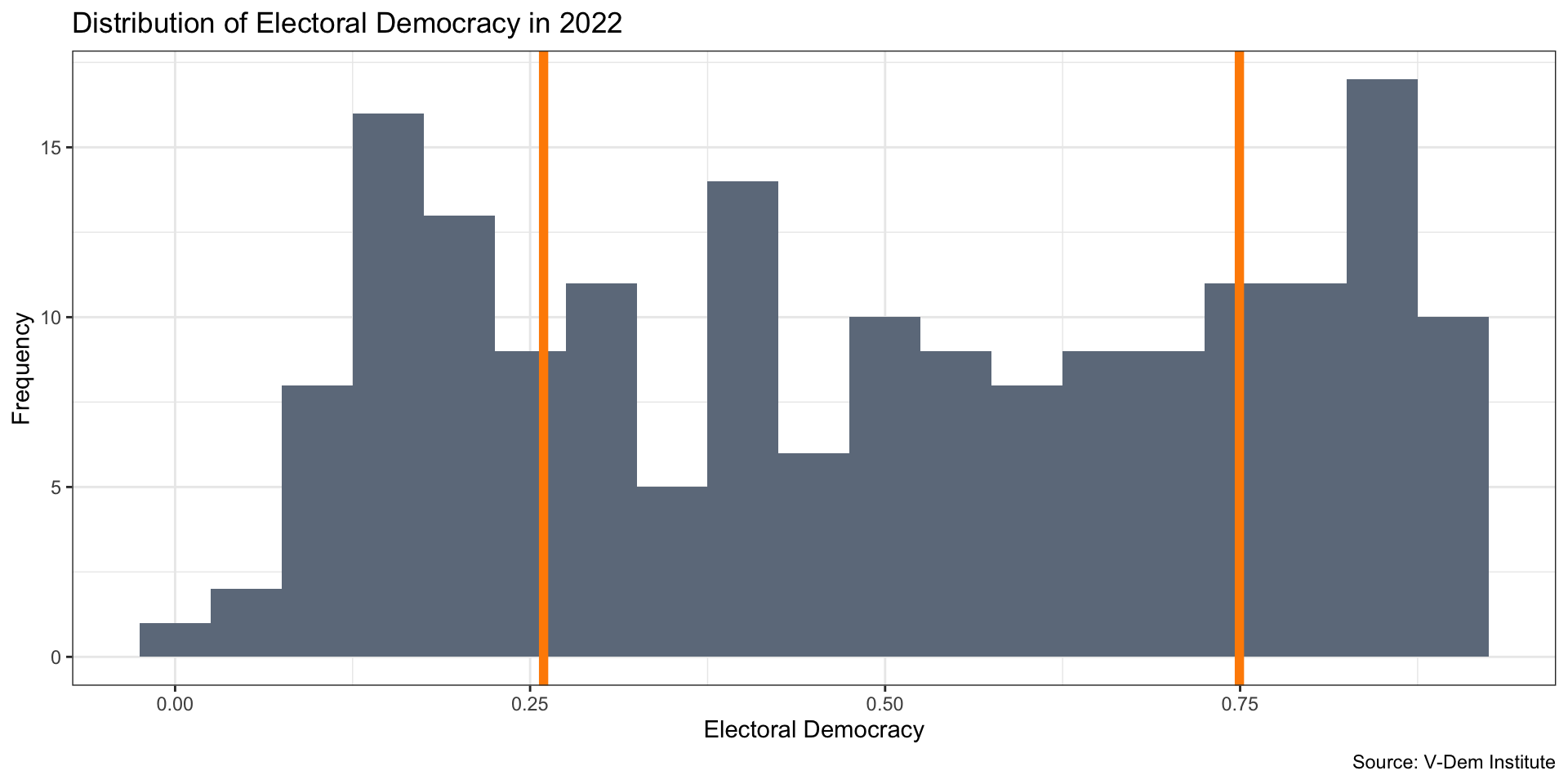
Interquartile Range

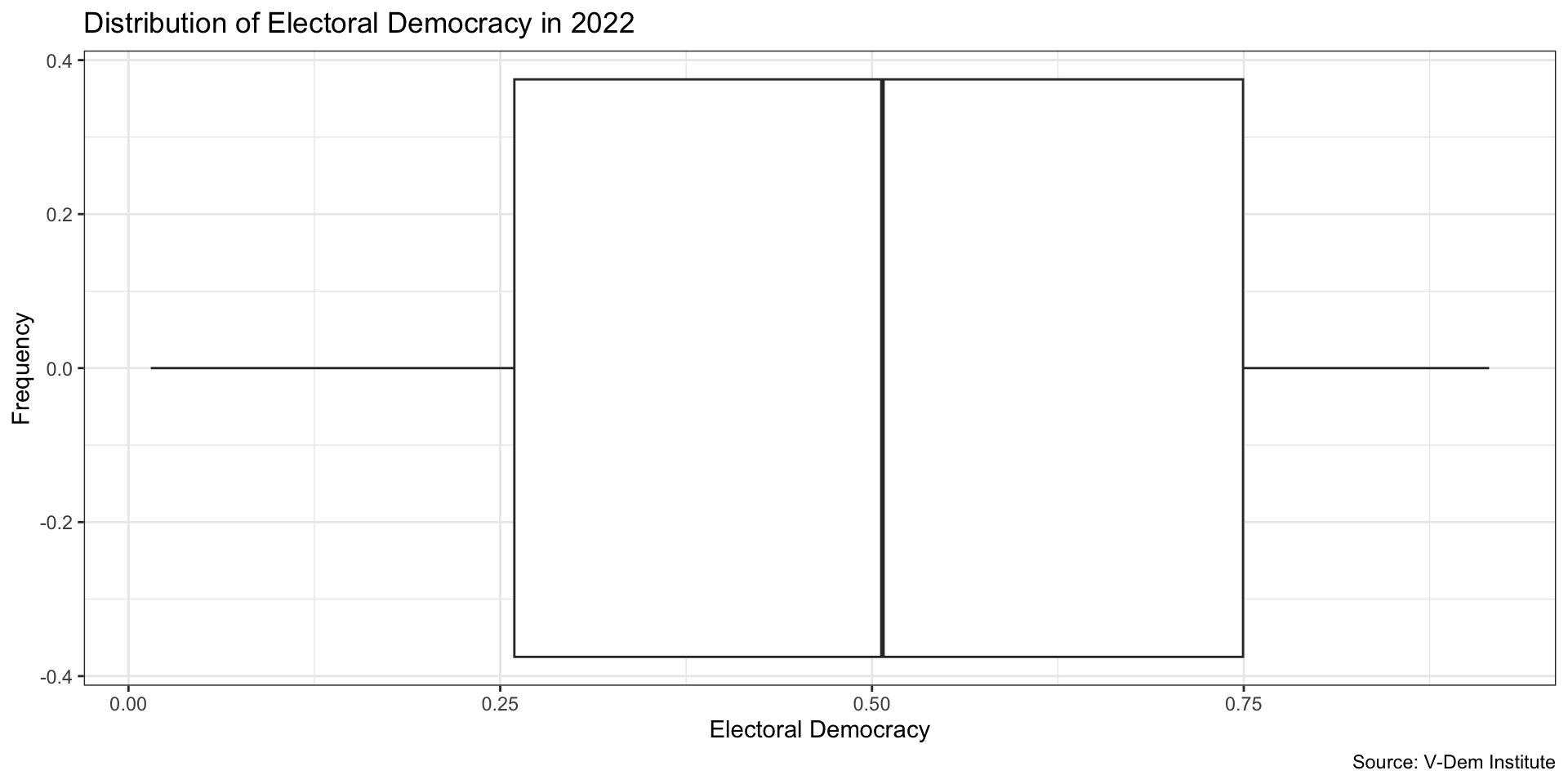
The middle 50 percent of the countries in the data lie between 0.262 and 0.747

The range length of 0.485 tells us something about the spread of the distribution

vdem2022 %>% 
  summarize(IQRlow =  quantile(v2x_polyarchy, .25),
            IQRhigh = quantile(v2x_polyarchy, .75),
            IQRlength = IQR(v2x_polyarchy)
          )
  IQRlow IQRhigh IQRlength
1 0.2595  0.7495      0.49

The Box Plot

Code 
ggplot(vdem2022, aes(x = v2x_polyarchy )) +
  geom_boxplot() + 
  theme_bw() +
   labs(
    x = "Electoral Democracy", 
    y = "Frequency", 
    title = "Distribution of Electoral Democracy in 2022", 
    caption = "Source: V-Dem Institute"
  )

Measure of Spead: Standard Deviation


  • Standard deviation

  • Can think of this as something like the “average distance” of each data point from the mean

Measure of Spead: Standard Deviation


  • Can think of this as something like the “average distance” of each data point from the mean
vdem2022 %>% 
  summarize(mean = mean(v2x_polyarchy),
            stdDev = sd(v2x_polyarchy))
       mean    stdDev
1 0.4977821 0.2621028

Standard Deviation Simple Example

x = c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
mean(x)
[1] 5

Standard Deviation Simple Example


  • First, we calculate the variance:
  • For each point, we calculate the deviation from the mean: \[e_i = X_i - mean(X)\]
    • For the point where the value is 0, this is: 0-5 = -5
    • For the point where the value is 10, this is: 10-5 = 5
  • Then we square all of the \(e_i\) –> \(e_i^2\), and add them up
    • Why do we square them?

Standard Deviation Simple Example


  • Then we divide by \(N-1\), the number of observations, to get an average squared deviation from the mean

  • Finally, to get standard deviation, then take the square root of the variance

    • This transforms the variance back into the units of the original variable (it basically undoes the squaring we did before)

Standard Deviation Simple Example

x = c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
e <- x - mean(x)
e
 [1] -5 -4 -3 -2 -1  0  1  2  3  4  5

Standard Deviation Simple Example

x = c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
e_squared <- e^2
e_squared
 [1] 25 16  9  4  1  0  1  4  9 16 25

Standard Deviation Simple Example

x = c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
sum_e_squared <- sum(e_squared)
sum_e_squared
[1] 110

Standard Deviation Simple Example

variance <- sum_e_squared/(length(x)-1)
variance
[1] 11

Standard Deviation Simple Example

standard_dev <- sqrt(variance)
standard_dev
[1] 3.316625
sd(x)
[1] 3.316625

Questions?

Calculating Statistics by groups


  • What if we want to describe electoral democracy and see how it differs by some different variable? For example, by world region, or by year?

Calculating Statistics by groups

  • Let’s calculate the mean and median of electoral democracy in each world region

  • For this, we add the group_by() to our previous code

vdem2022 %>% 
  group_by(region) %>% 
  summarize(mean_dem = mean(v2x_polyarchy),
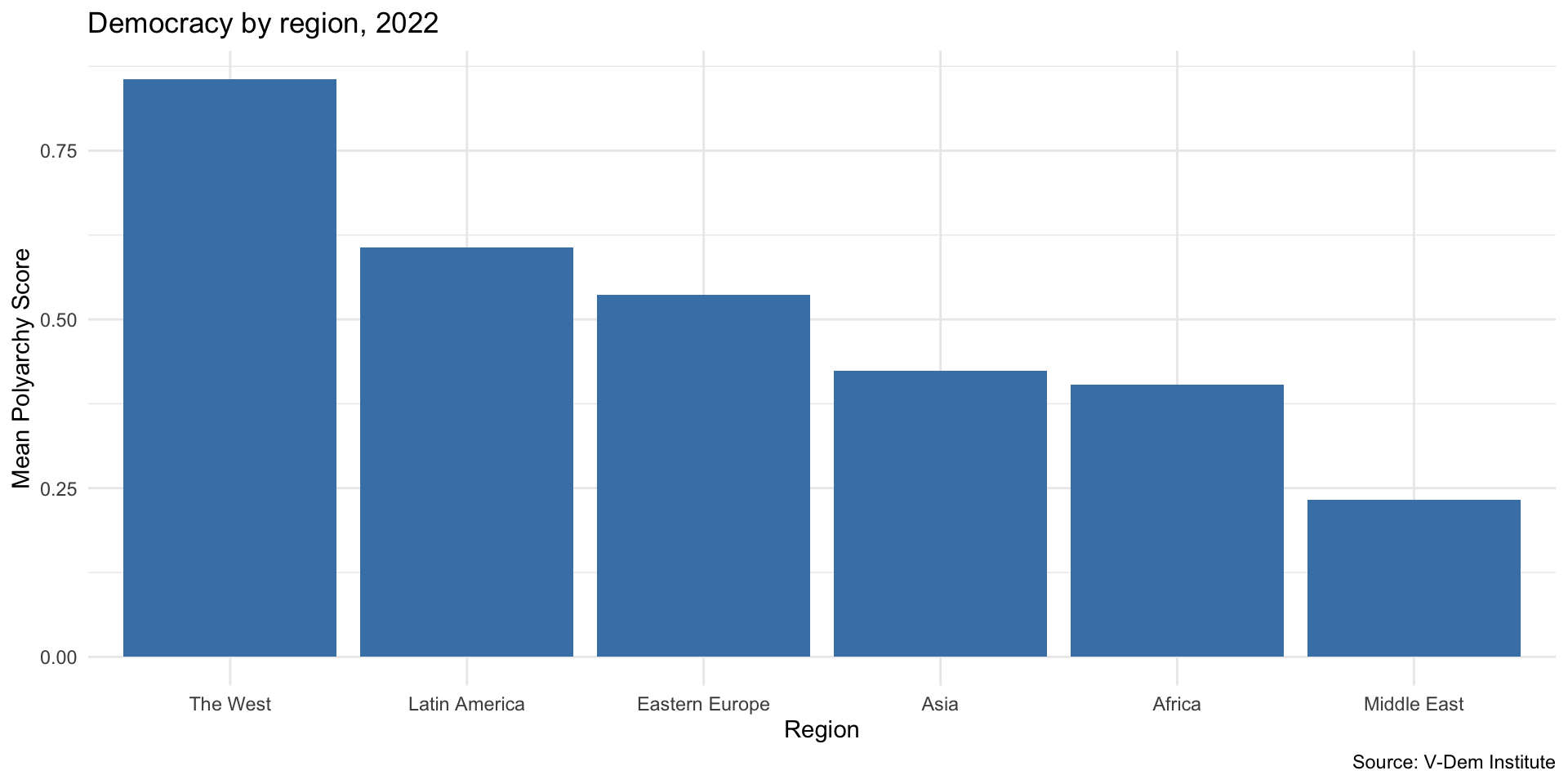
            median_dem = median(v2x_polyarchy))
# A tibble: 6 × 3
  region         mean_dem median_dem
  <chr>             <dbl>      <dbl>
1 Africa            0.403      0.377
2 Asia              0.423      0.412
3 Eastern Europe    0.537      0.564
4 Latin America     0.607      0.685
5 Middle East       0.232      0.208
6 The West          0.856      0.855

Calculating Statistics by groups

  • Let’s store our statistics as a new data object, democracy_region
democracy_region <- vdem2022 %>% 
  group_by(region) %>% 
  summarize(mean_dem = mean(v2x_polyarchy),
            median_dem = median(v2x_polyarchy))

democracy_region
# A tibble: 6 × 3
  region         mean_dem median_dem
  <chr>             <dbl>      <dbl>
1 Africa            0.403      0.377
2 Asia              0.423      0.412
3 Eastern Europe    0.537      0.564
4 Latin America     0.607      0.685
5 Middle East       0.232      0.208
6 The West          0.856      0.855

Visualize using a Bar Chart

Code 
ggplot(democracy_region, aes(x = reorder(region, -mean_dem), y = mean_dem)) +
  geom_col(fill = "steelblue") + 
  labs(
    x = "Region", 
    y = "Mean Polyarchy Score", 
    title = "Democracy by region, 2022", 
    caption = "Source: V-Dem Institute"
    ) + theme_minimal()

Break

Categorical Data

  • Data that fit in categories

  • Regime type

  • Region

  • Likert scale: Very Bad, Bad, Neutral, Good, Very Good

    • This kind of scale is ordinal: there is a natural ordering to the categories

V-Dem Regimes of the World Measure

  • Closed Autocracy
  • Electoral Autocracy
  • Electoral Democracy
  • Liberal Democracy

Data Setup

vdem2022 <- vdem2022 %>% 
  mutate(regime = case_match(v2x_regime,
                    0 ~ "Closed Autocracy",
                    1 ~ "Electoral Autocracy",
                    2 ~  "Electoral Democracy",
                    3 ~  "Liberal Democracy")
  )

Describe regimes of the world in 2022

We could take the mean ….

Describe regimes of the world in 2022

Wait, no we cannot

vdem2022 %>% 
  summarize(mean = mean(regime, na.rm = TRUE))
  mean
1   NA

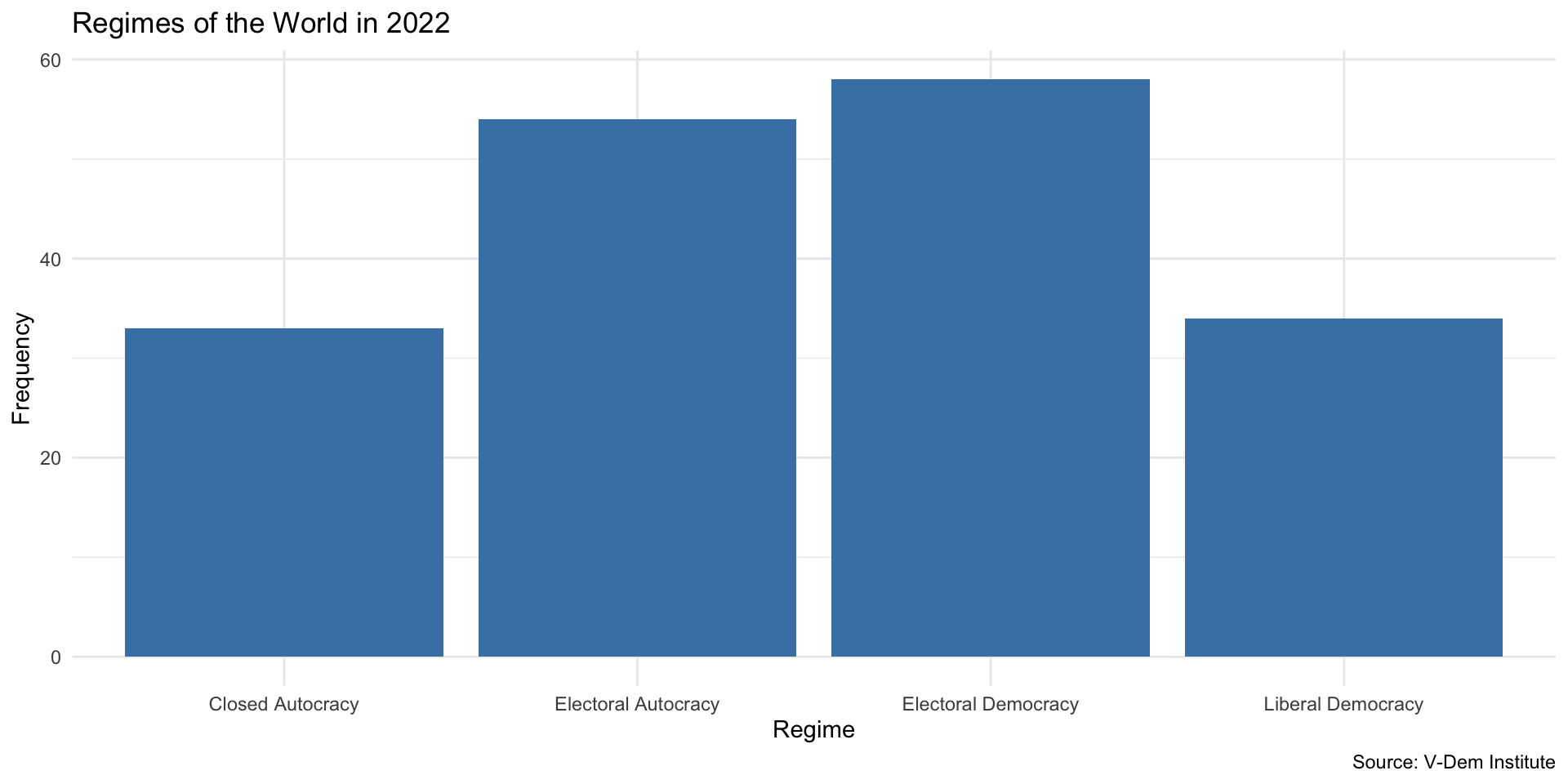
Describe regimes of the world in 2022

We could count the number of each regime type

vdem2022 %>% 
  count(regime)
               regime  n
1    Closed Autocracy 33
2 Electoral Autocracy 54
3 Electoral Democracy 58
4   Liberal Democracy 34

Describe regimes of the world in 2022

Contingency Table

library(gt)
count_regime <-vdem2022 %>% 
  count(regime)
gt(count_regime)
regime n
Closed Autocracy 33
Electoral Autocracy 54
Electoral Democracy 58
Liberal Democracy 34

Bar Plot is Usually Better

Code 
vdem2022 %>%
  ggplot(., aes(x = regime)) +
      geom_bar(fill = "steelblue") +
  theme_minimal() +
  labs(
    x = "Regime",
    y = "Frequency",
    title = "Regimes of the World in 2022",
    caption = "Source: V-Dem Institute"
  )

Summarizing a categorical variable by a goup

How do Regimes Vary by Region?

How do Regimes Vary by Region?

Code 
vdem2022 %>%
  ggplot(., aes(x = region, fill = regime)) +
      geom_bar() +
  theme_minimal() +
  labs(
    x = "Region",
    y = "Frequency",
    title = "Regimes of the World by World Region in 2022",
    caption = "Source: V-Dem Institute",
    fill = "Regime"
  )

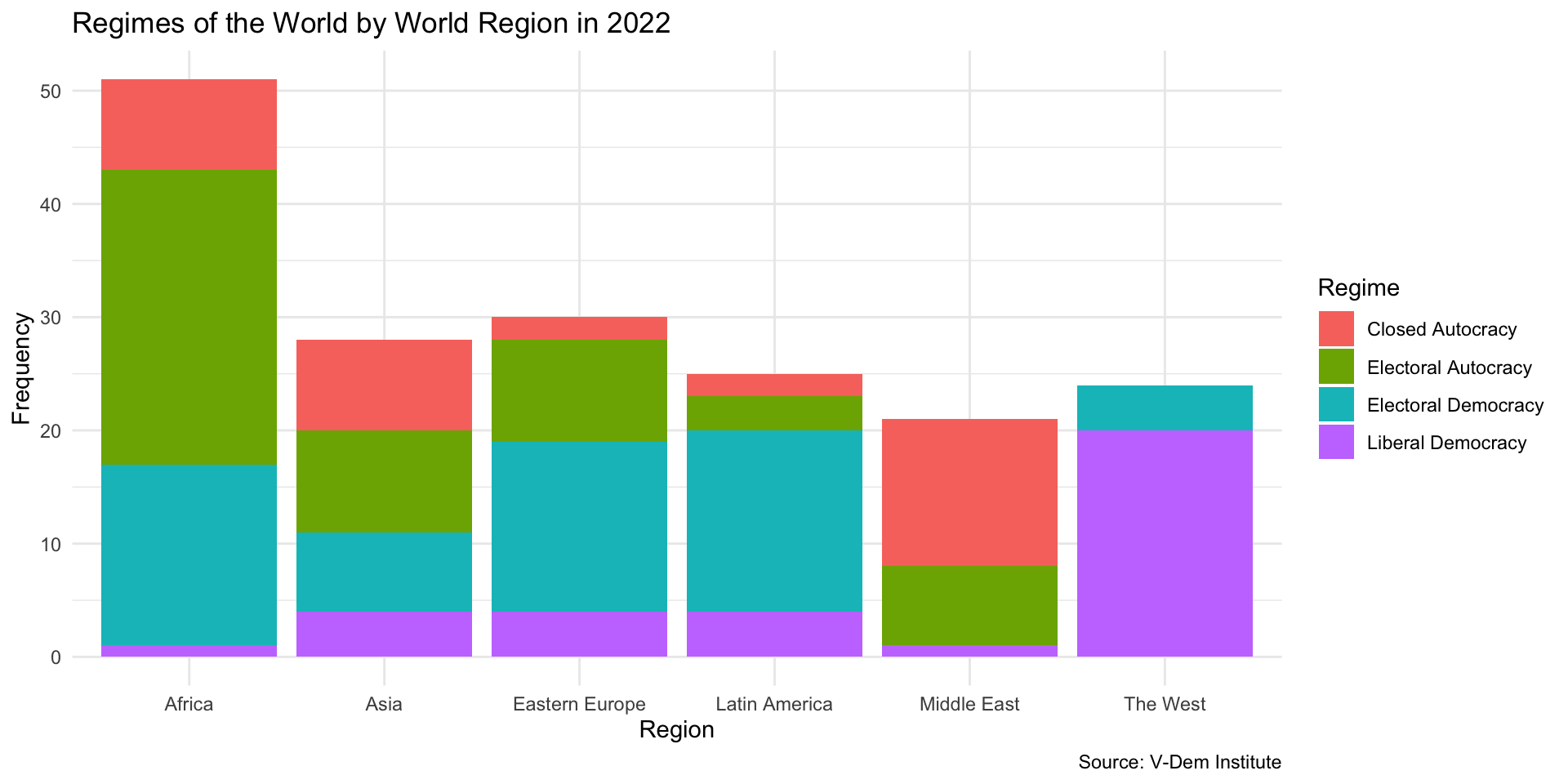
How could we improve this graph??

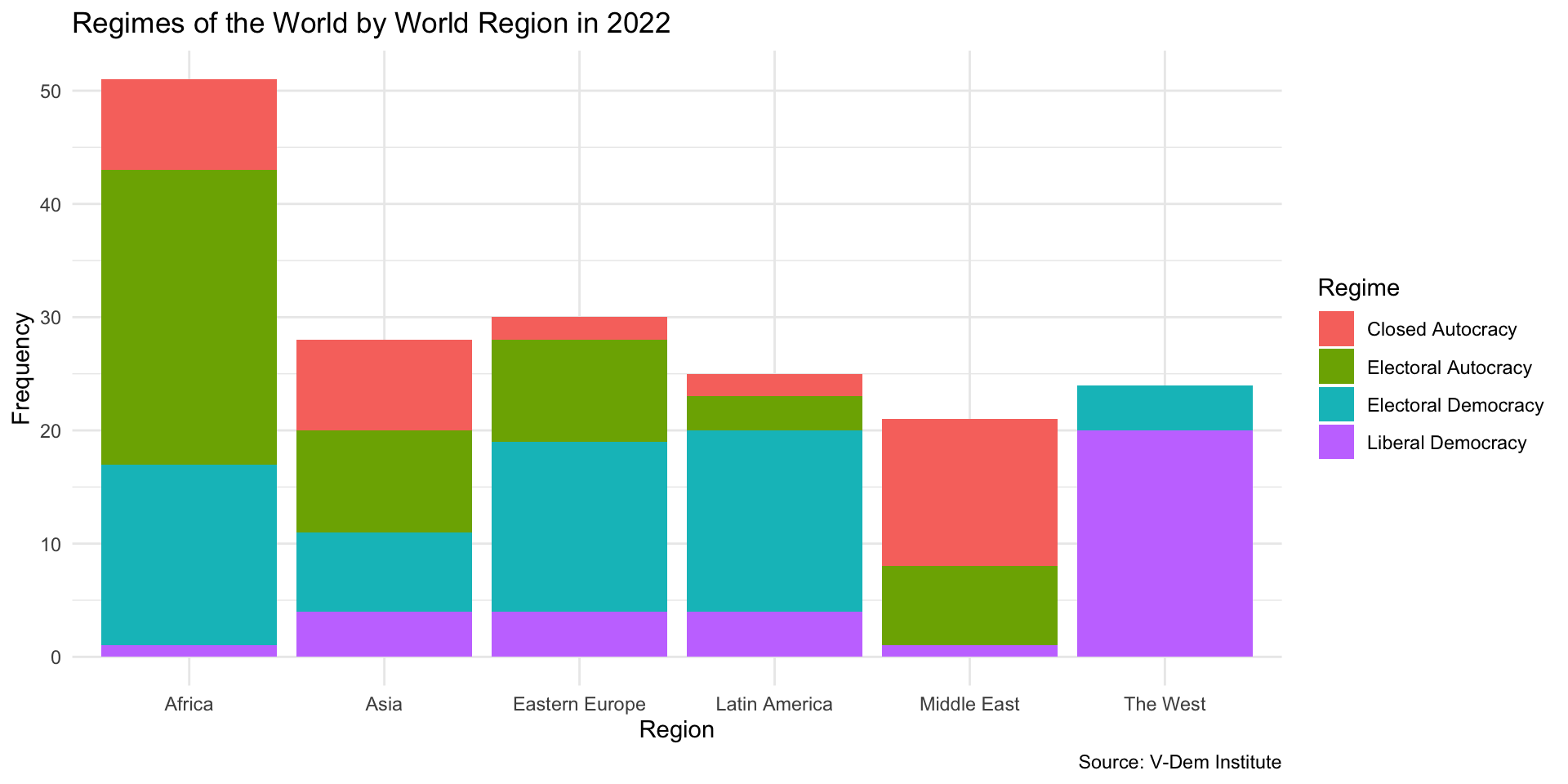
Colors need improving

Code 
vdem2022 %>%
  ggplot(., aes(x = region, fill = regime)) +
      geom_bar() +
  theme_minimal() +
  labs(
    x = "Region",
    y = "Frequency",
    title = "Regimes of the World by World Region in 2022",
    caption = "Source: V-Dem Institute",
    fill = "Regime"
  ) +
  scale_fill_viridis_d(option = "D")

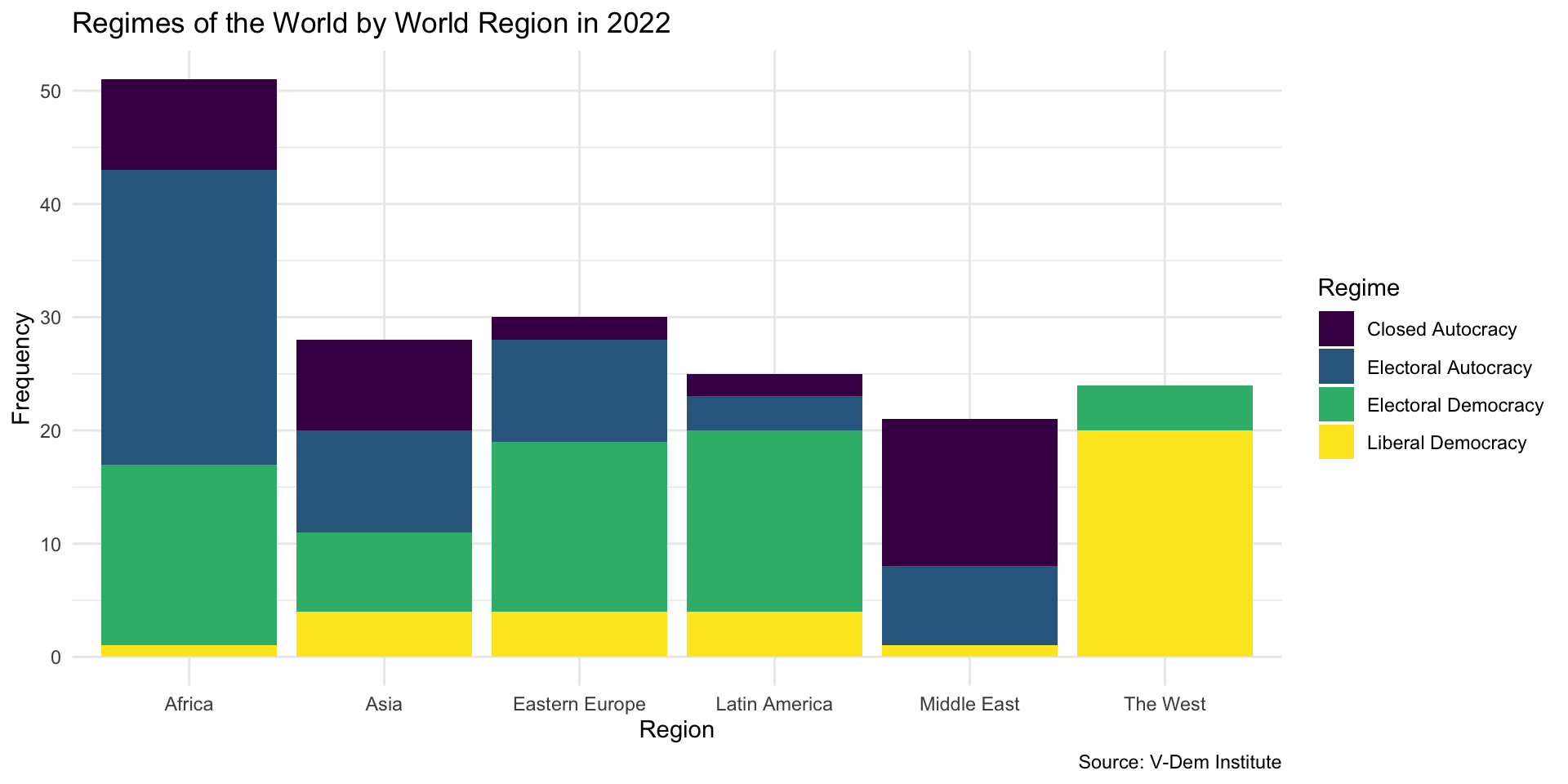
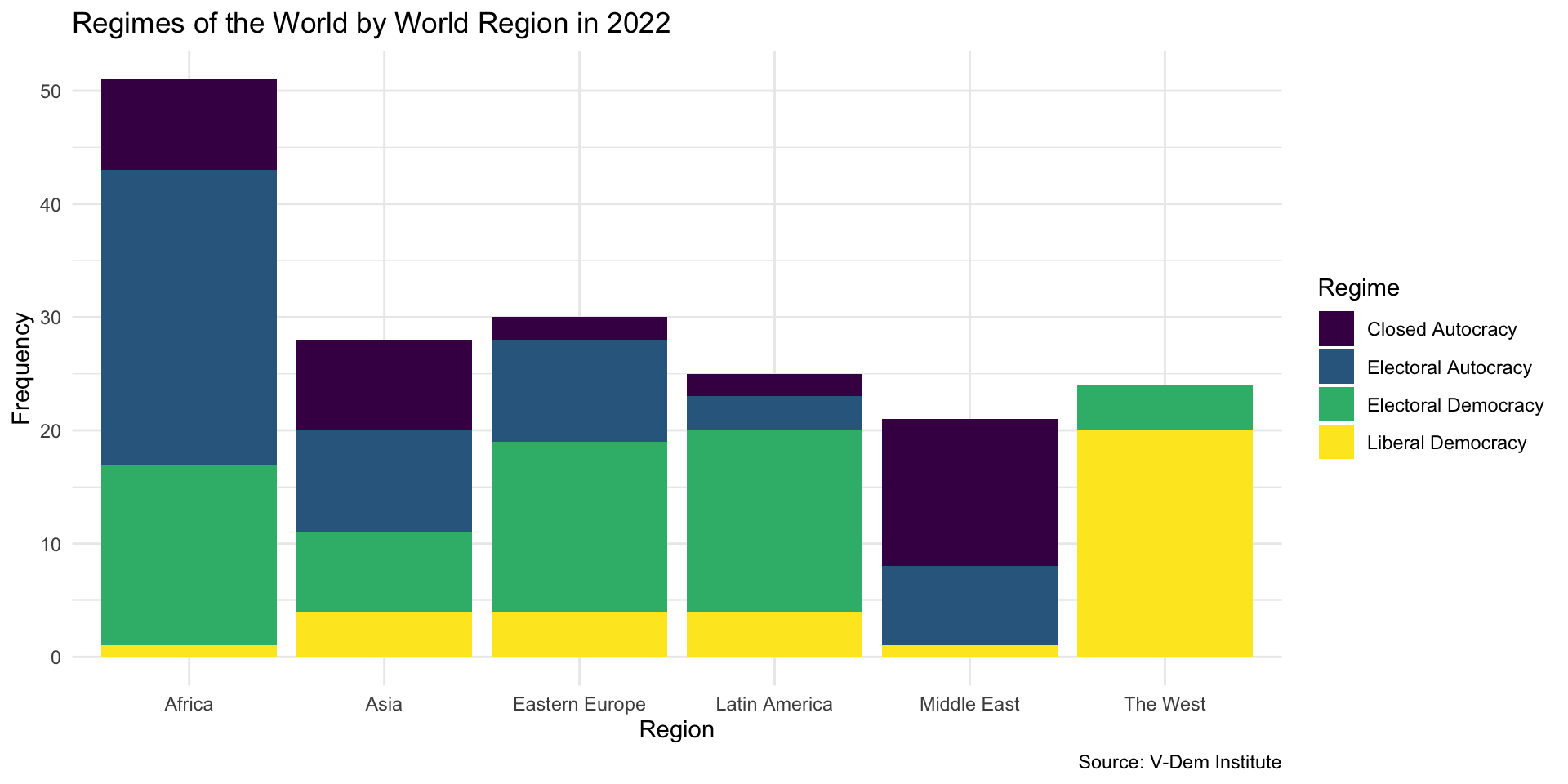
Region Size

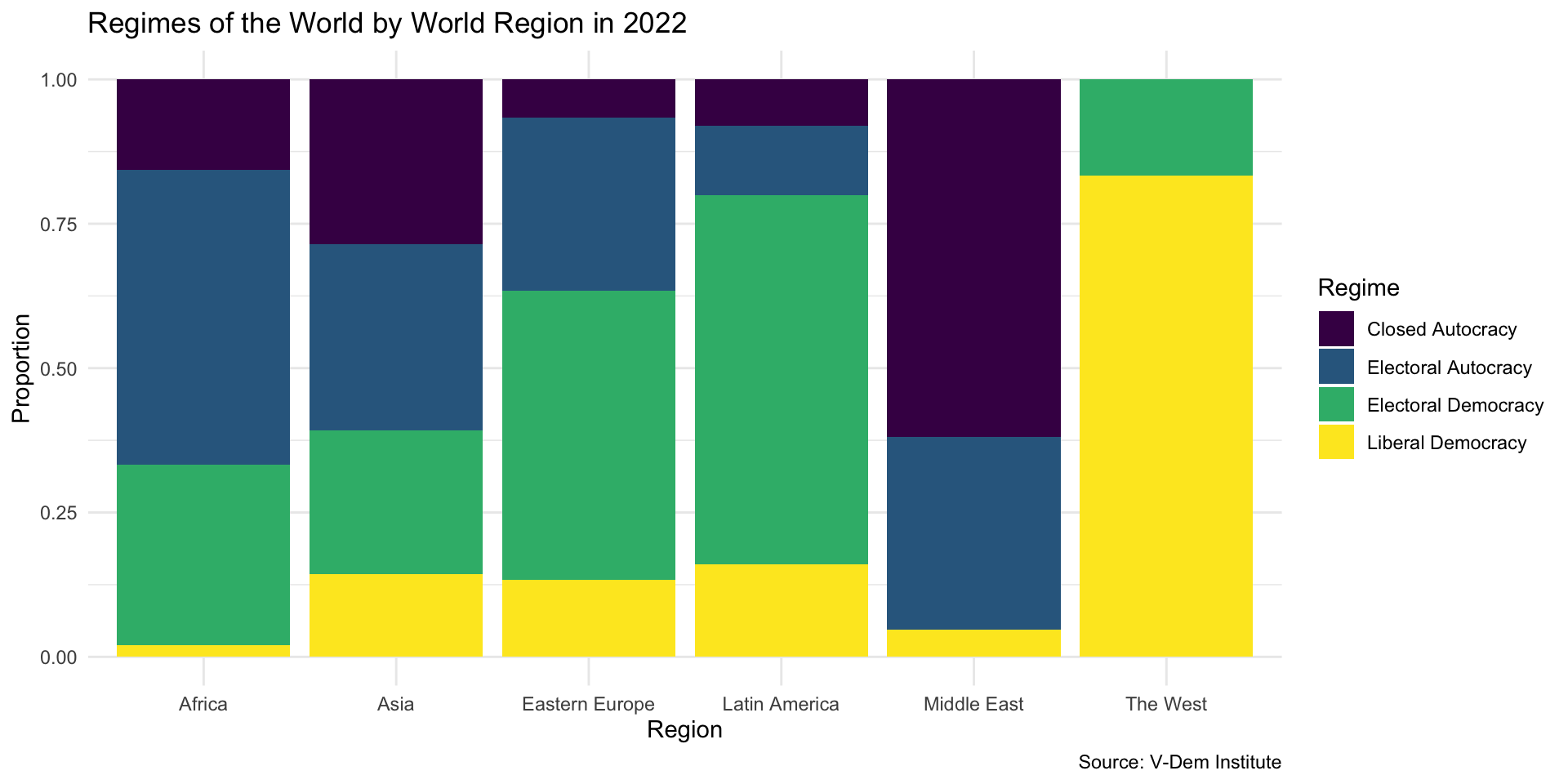
Some regions have more countries than others. Why does this create an issue for telling a story with our data here?

Is this better?

Code 
vdem2022 %>%
  ggplot(., aes(x = region, fill = regime)) +
      geom_bar(position = "fill") +
  theme_minimal() +
  labs(
    x = "Region",
    y = "Proportion",
    title = "Regimes of the World by World Region in 2022",
    caption = "Source: V-Dem Institute",
    fill = "Regime"
  ) +
  scale_fill_viridis_d(option = "D")

Numerical Variable by Group

How should we interpret this plot?

Code 
library(ggridges)
library(forcats)
  ggplot(vdem2022, aes(x = v2x_polyarchy, y = region)) +
           geom_density_ridges(fill = "steelblue3") +
      labs(
    x = "Electoral Democracy",
    y = "Region",
    title = "A Ridge Plot",
    caption = "Source: V-Dem Institute",
  ) +
    theme_bw()

Posit Cloud

IAFF 6501 Website