Modeling

January 29, 2025

Modeling

  • Use models to explain the relationship between variables and to make predictions

  • Explaining relationships [usually interested in causal relationships, but not always]

    • Does oil wealth impact regime type?

  • Predictive modeling

    • Where is violence most likely to happen in [country X] during their next election?

    • Is this email spam?

Modeling

Modeling

Example: GDP per capita and Democracy

Pull in the VDEM Data

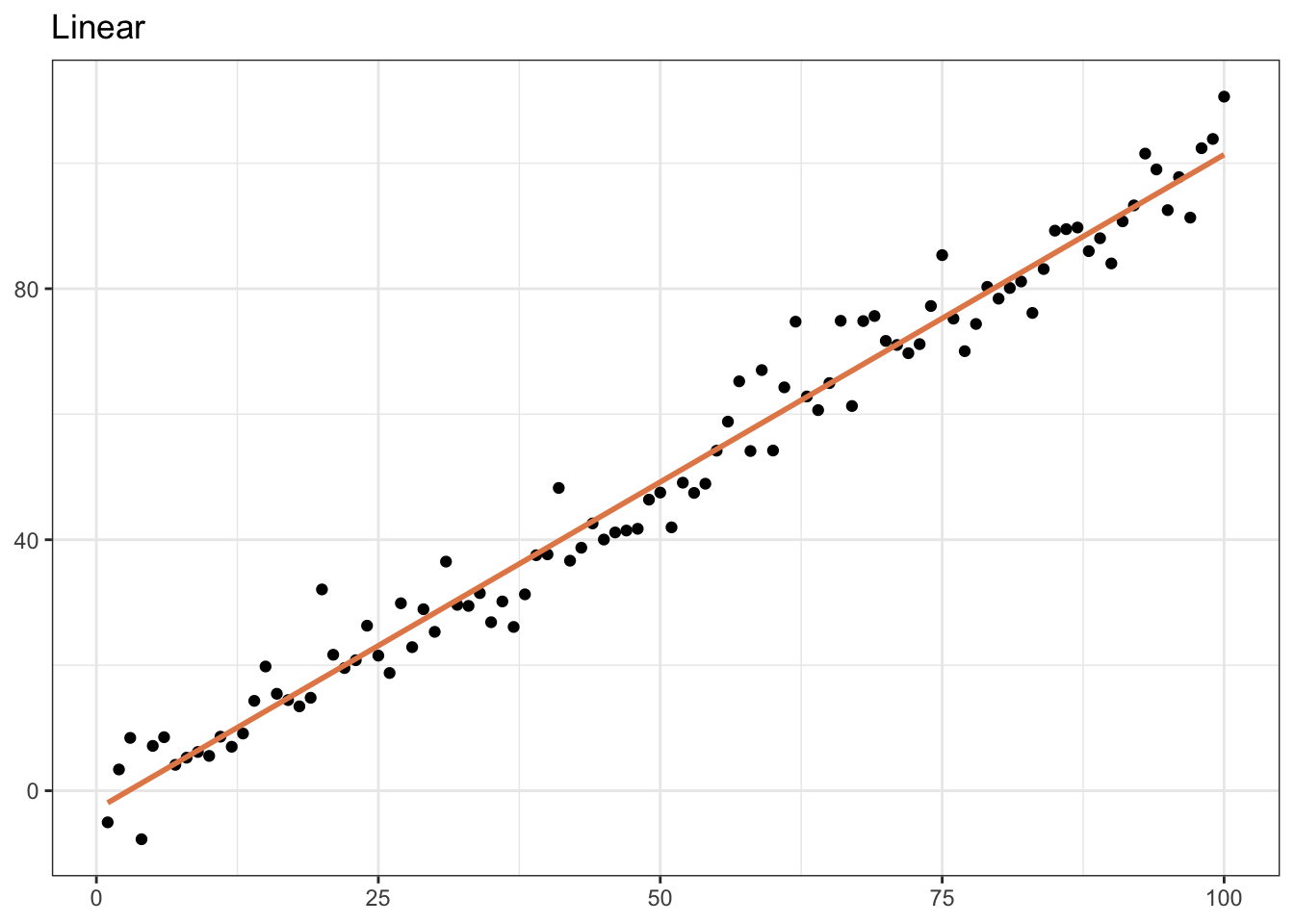
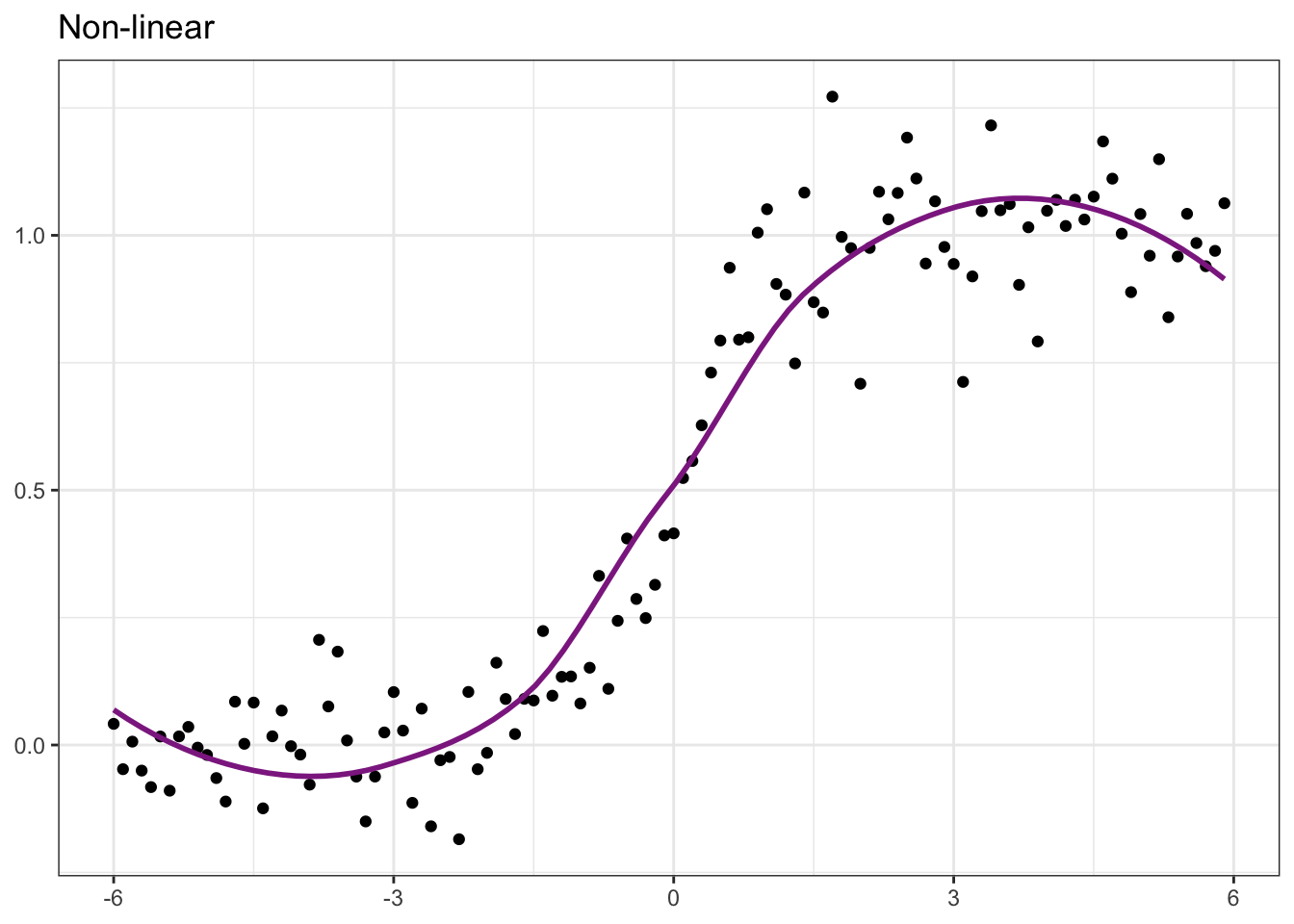
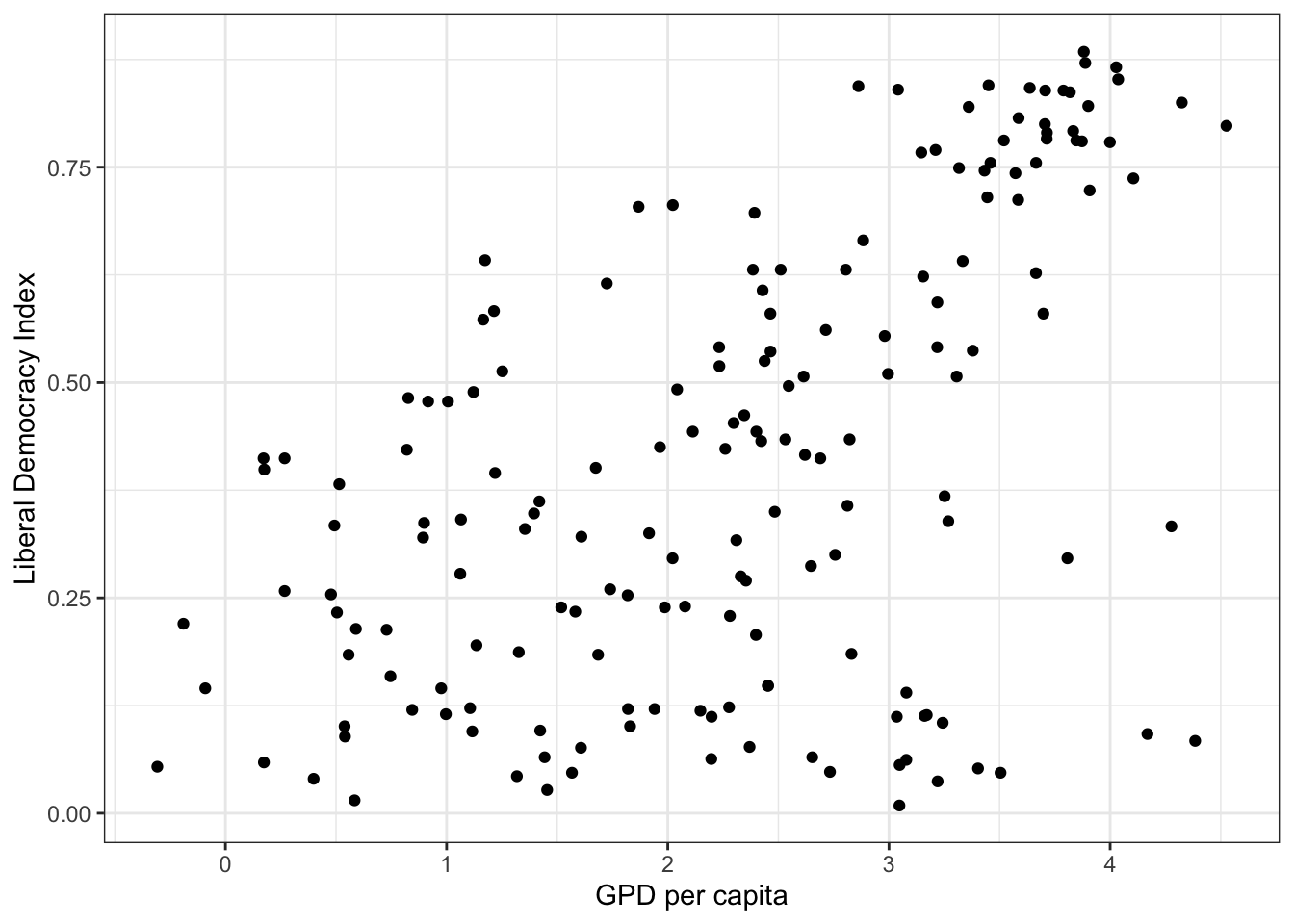
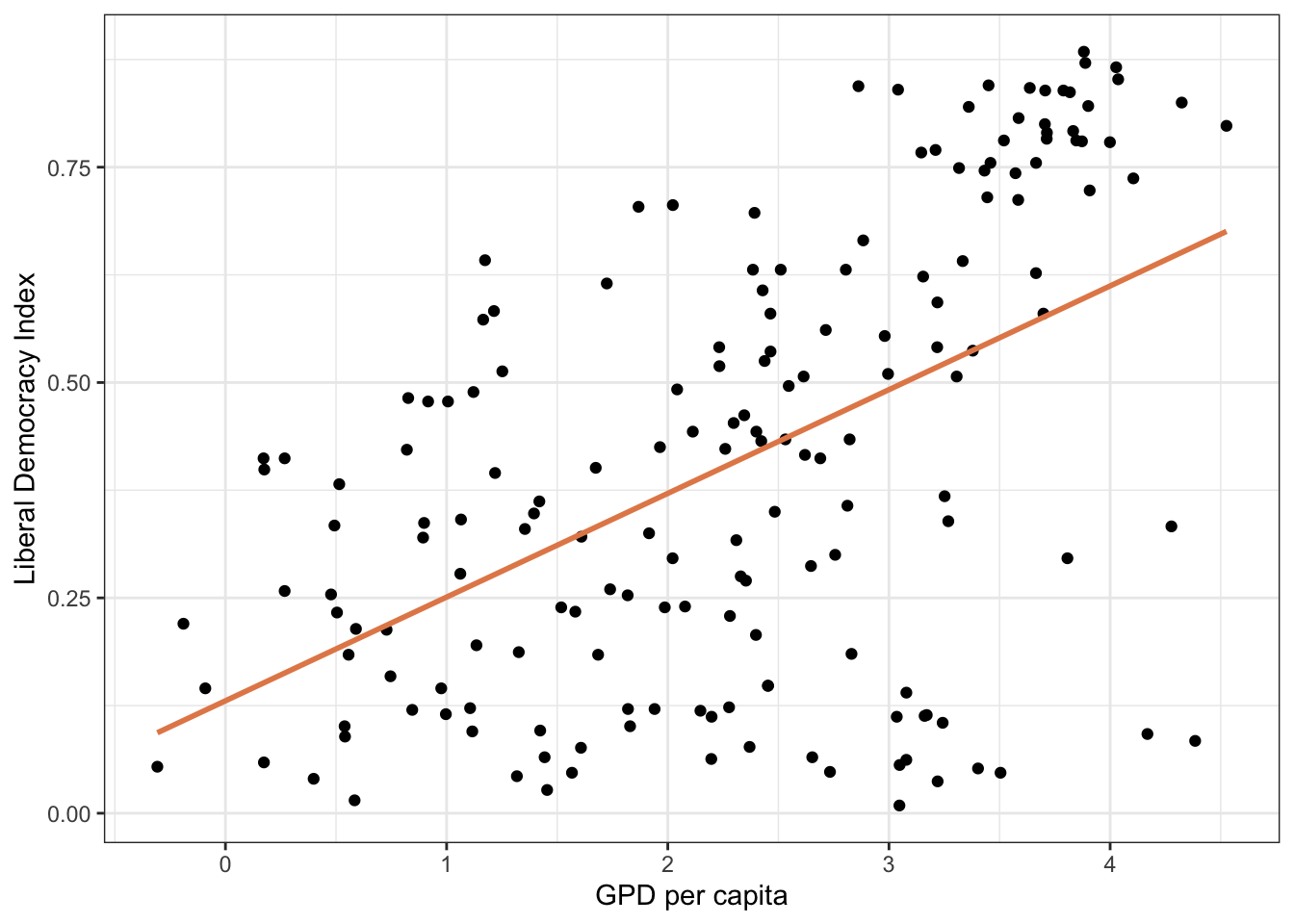
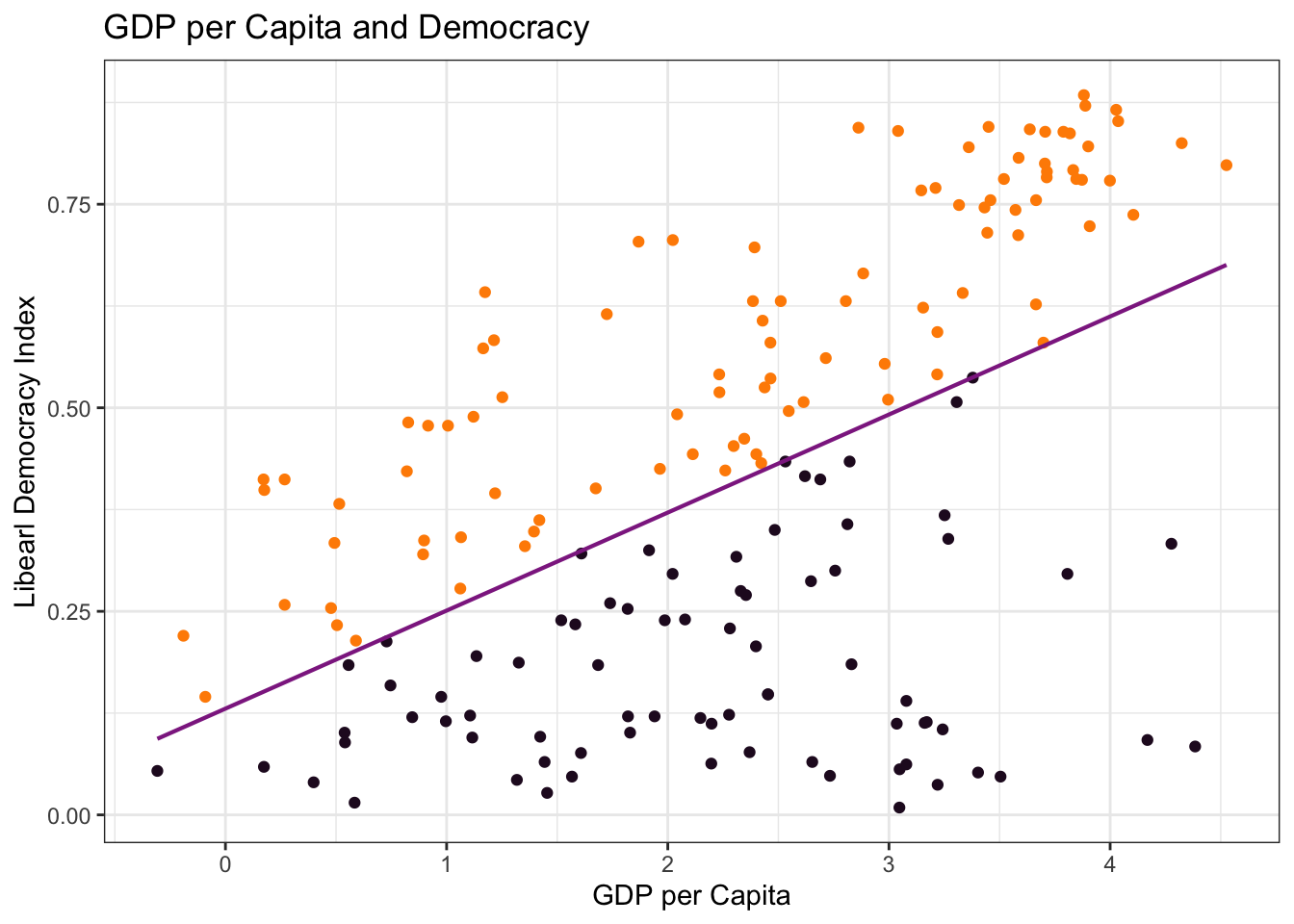
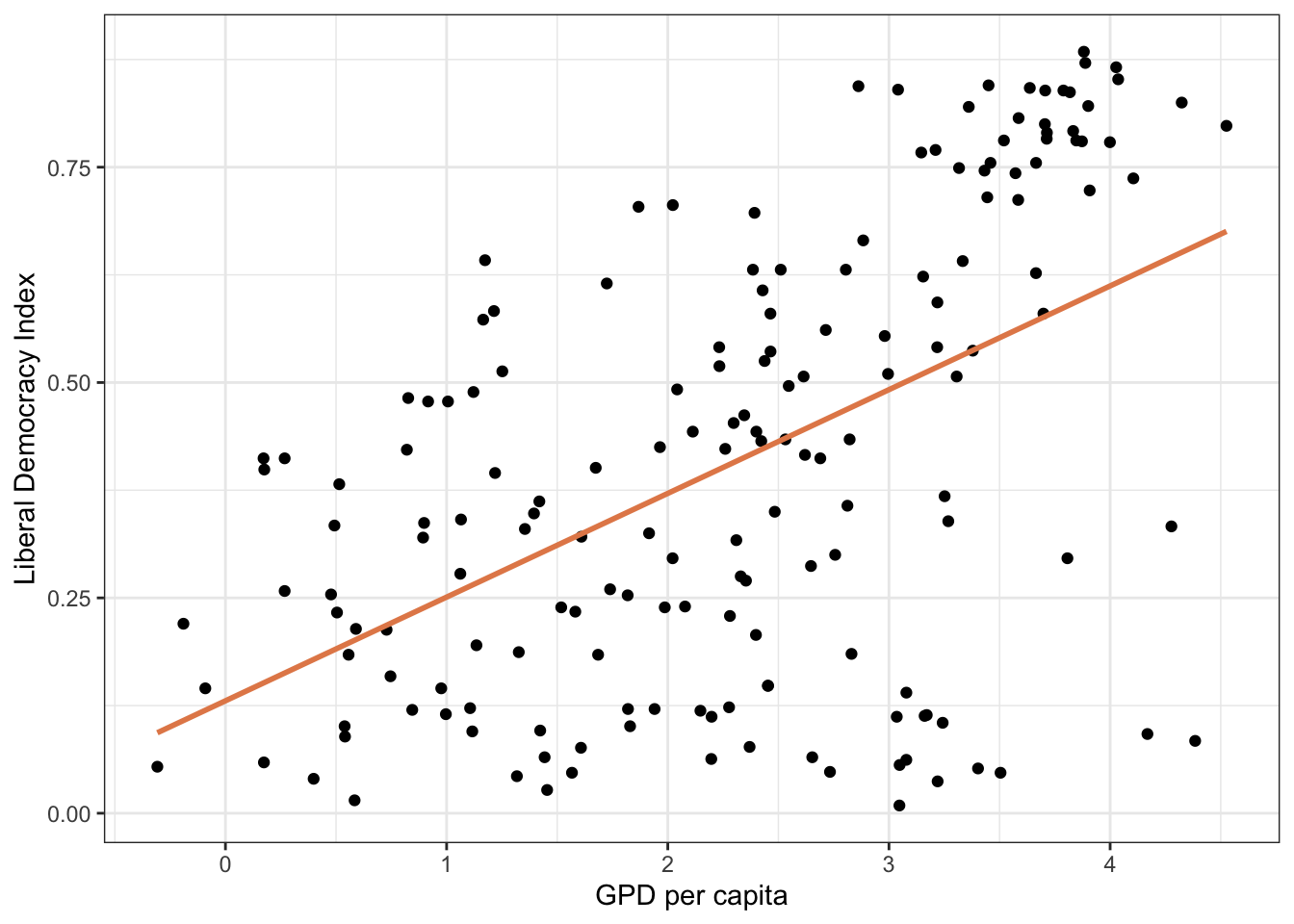
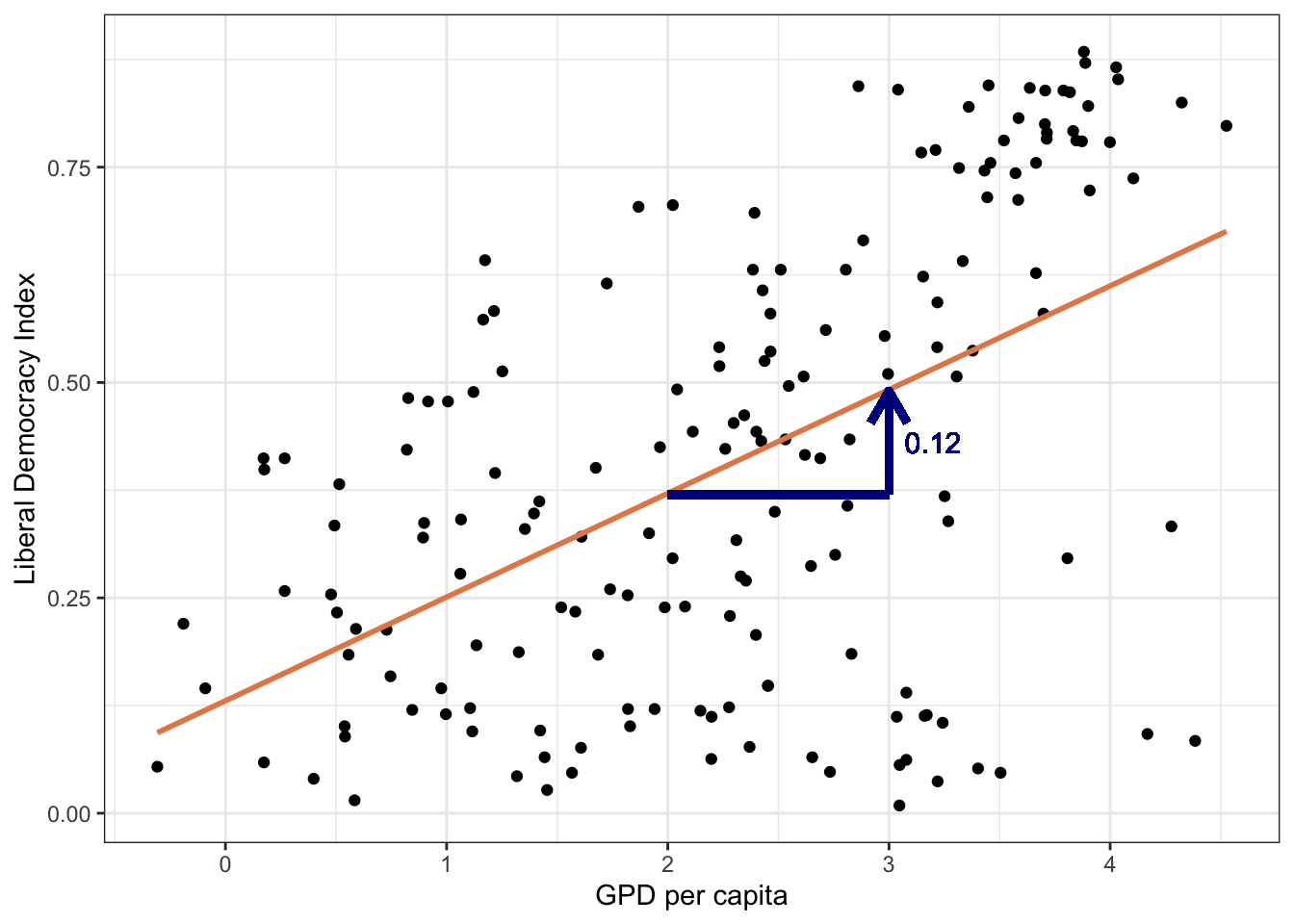
library(vdemdata)
modelData <- vdem %>% 
  filter(year == 2019) %>% 
  select(country_name, v2x_libdem, e_gdppc) %>% 
  mutate(lg_gdppc = log(e_gdppc))
glimpse(modelData)
Rows: 179
Columns: 4
$ country_name <chr> "Mexico", "Suriname", "Sweden", "Switzerland", "Ghana", "…
$ v2x_libdem   <dbl> 0.434, 0.580, 0.871, 0.866, 0.615, 0.607, 0.755, 0.260, 0…
$ e_gdppc      <dbl> 16.814, 11.752, 48.804, 56.110, 5.608, 11.345, 39.061, 5.…
$ lg_gdppc     <dbl> 2.8222119, 2.4640234, 3.8878123, 4.0273140, 1.7241941, 2.…

Visualize first!

Add a trend line

Models as functions

  • We can represent relationships between variables using functions

  • A function is a mathematical concept: the relationship between an output and one or more inputs

    • Plug in the inputs and receive back the output

Models as functions

  • Example: The formula \(y = 3x + 7\) is a function with input \(x\) and output \(y\).

    • If \(x\) is \(5\), \(y\) is \(22\),
    • \(y = 3 \times 5 + 7 = 22\)

Language

  • Response variable: Variable whose behavior or variation you are trying to understand, on the y-axis in the plot

    • Dependent variable
    • Outcome variable
    • Y variable

Language

  • Explanatory variables: Other variables that you want to use to explain the variation in the response, on the x-axis in the plot

    • Independent variables
    • Predictors

Linear Model with One Explanatory Variable

  • \(Y = a + bX\)
  • \(Y\) is the outcome variable
  • \(X\) is the explanatory variable
  • \(a\) is the intercept: the predicted value of \(Y\) when \(X\) is equal to 0
  • \(b\) is the slope of the line [remember rise over run!]

Language

  • Predicted value: Output of the model function

    • The model function gives the typical (expected) value of the response variable conditioning on the explanatory variables

    • We often call this \(\hat{Y}\) to differentiate the predicted value from an observed value of Y in the data

Language

  • Residuals: A measure of how far each case is from its predicted value (based on a particular model)
    • Residual = Observed value (\(Y\)) - Predicted value (\(\hat{Y}\))
    • How far above/below the expected value each case is

Residuals

Linear Model

\(\hat{Y} = a + bX\)

Linear Model

\(\hat{Y} = 0.13 + 0.12 X\)

Linear Model: Interpretation

  • \(\hat{Y} = a + b \times X\)

  • \(\hat{Y} = 0.13 + 0.12 \times X\)

  • How to interpret our estimate of \(a\)?

  • \(\hat{Y} = 0.13 + 0.12 \times 0\)

  • \(\hat{Y} = 0.13\)

a is our predicted level of democracy when GDP per capita is 0.

Linear Model: Interpretation

  • \(\hat{Y} = a + b \times X\)

  • \(\hat{Y} = 0.13 + 0.12 \times X\)

  • How to interpret our estimate of \(b\)?

  • \(\hat{Y} = a + \frac{Rise}{Run} \times X\)

  • \(\hat{Y} = a + \frac{Change Y}{Change X} \times X\)

Linear Model: Interpretation

  • \(b = \frac{Change Y}{Change X}\)

  • \(0.12 = \frac{Change Y}{Change X}\)

  • \(0.12 * {ChangeX} = {Change Y}\)

Linear Model: Interpretation

  • \(0.12 * {ChangeX} = {Change Y}\)

When \(ChangeX = 1\):

  • \(0.12 = {Change Y}\)
  • \(b\) is the predicted change in \(Y\) associated with a ONE unit change in X.

Linear Model: Interpretation

Linear Model: Interpretation

Linear Model: Interpretation

Linear Model: Interpretation


Is this the causal effect of GDP per capita on liberal democracy?

Correlation vs Causation


  • The model tells us the association between variables.
  • There could be reverse or cyclical causation: maybe liberal democracy causes GDP per capita (not vice versa)

  • There could be an omitted factor (z) that causes both GDP per capita and liberal democracy.

    • If true, this is a spurious correlation

Questions for you


An economist is interested in the relationship between years of education (X) and hourly wages in dollars (Y). They estimate a linear model with estimates of \(a\) and \(b\) as follows:

\(\hat{Y} = 9 + 1.60*{YrsEducation}\)

  • Write a sentence to interpret the estimate of \(a\) (the intercept)

  • Write a sentence to interpret the estimate of \(b\) (the slope, or coefficient on YrsEducation)

  • What is the predicted hourly wage for those with 10 years of education?

  • Should you interpret this as a causal effect of education? Why or why not?

Intercept


\(\hat{Y} = 9 + 1.60*{YrsEducation}\)

The model predicts that people with \(0\) years of education will make 9 dollars an hour.

Slope


\(\hat{Y} = 9 + 1.60*{YrsEducation}\)

The model predicts that a one year increase in years of education will result in an additional 1.60 dollars per hour in earnings.

Predicted Hourly Wage for 10 yrs Education

9 + 1.6*10
[1] 25

Next step

  • Linear model with one predictor: \(Y = a + bX\)

  • How do we figure out what the best values are for \(a\) and \(b\)??

IAFF 6501 Website