IAFF 6501 – Modeling

Pull in the VDEM Data

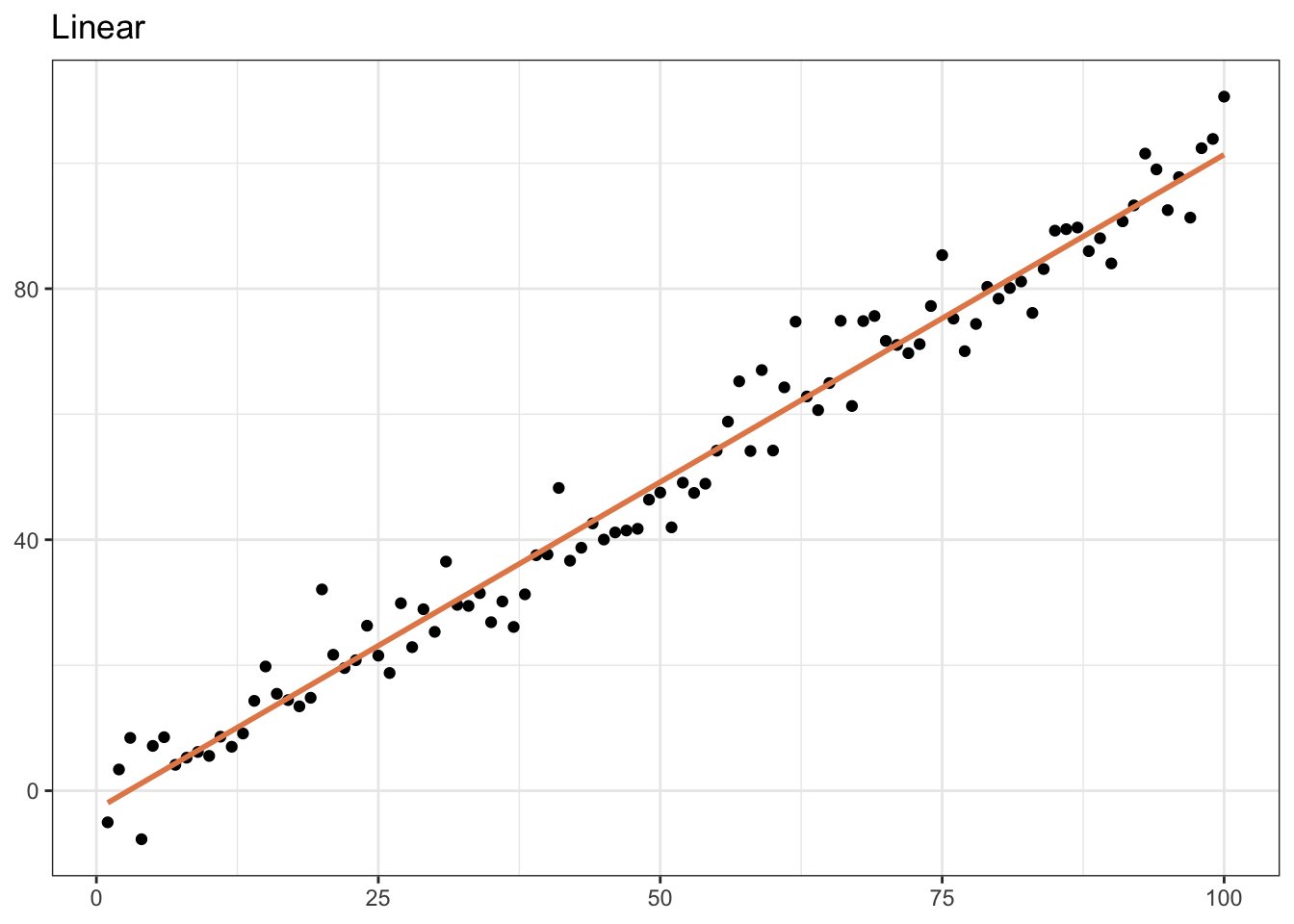
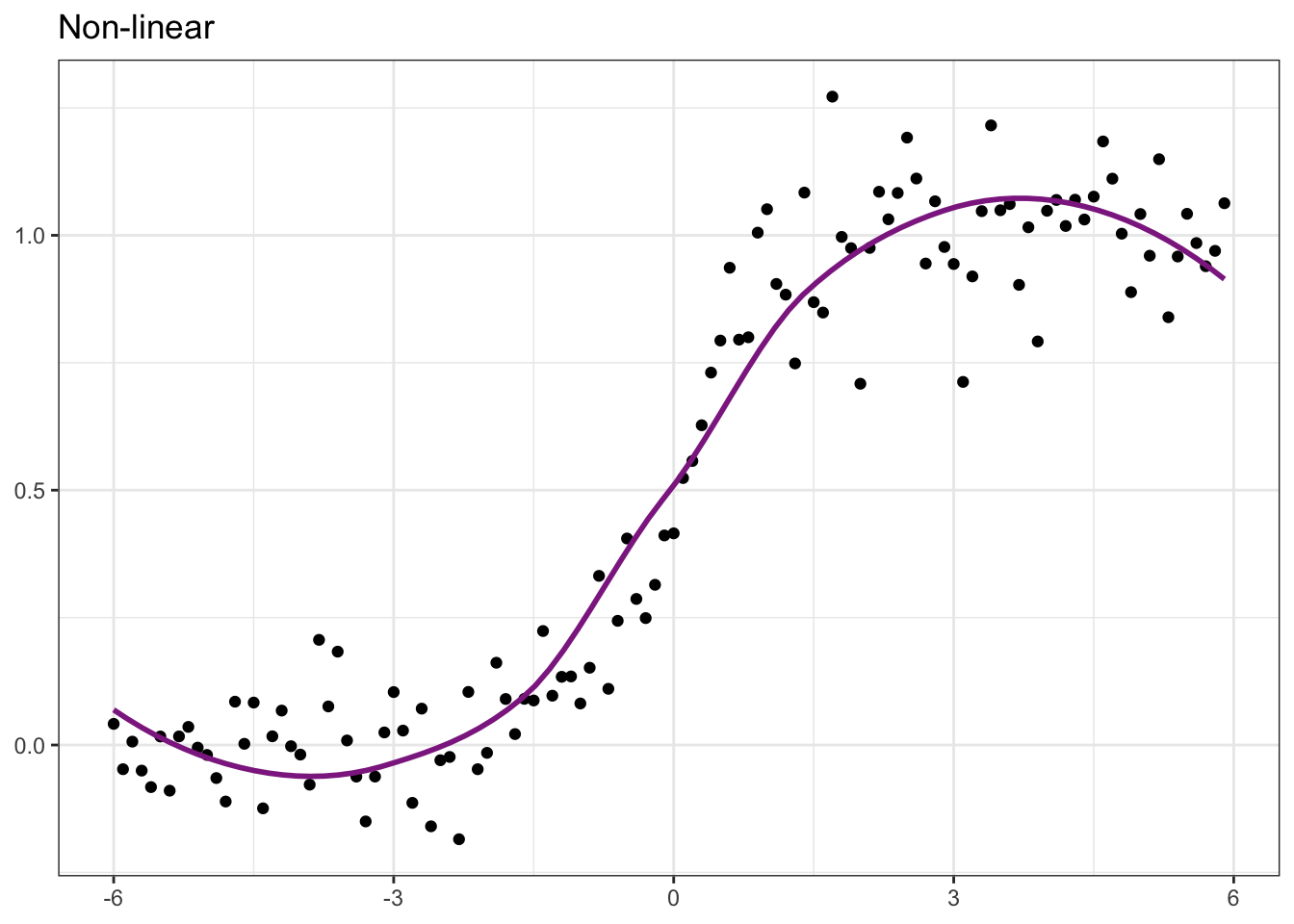
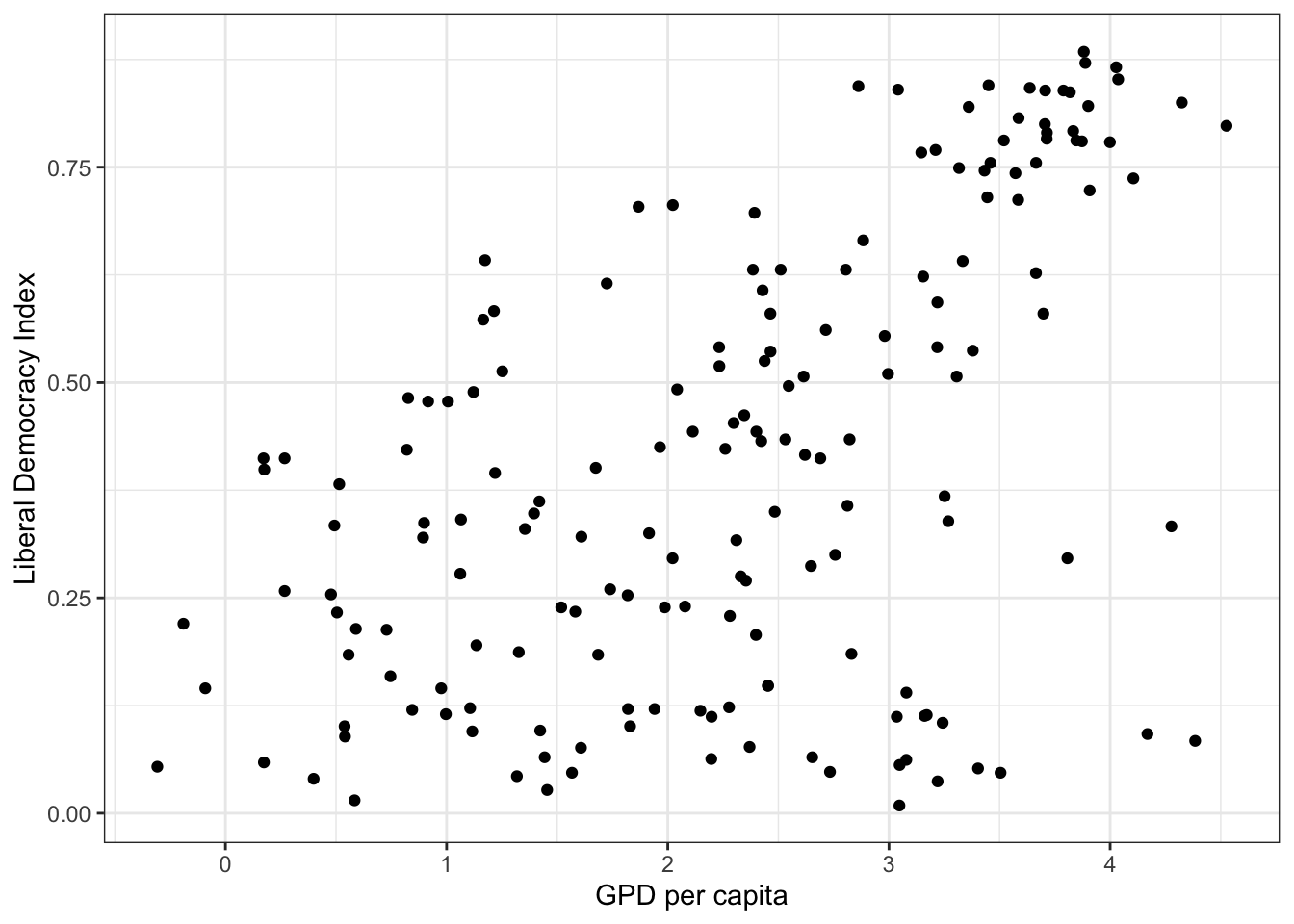
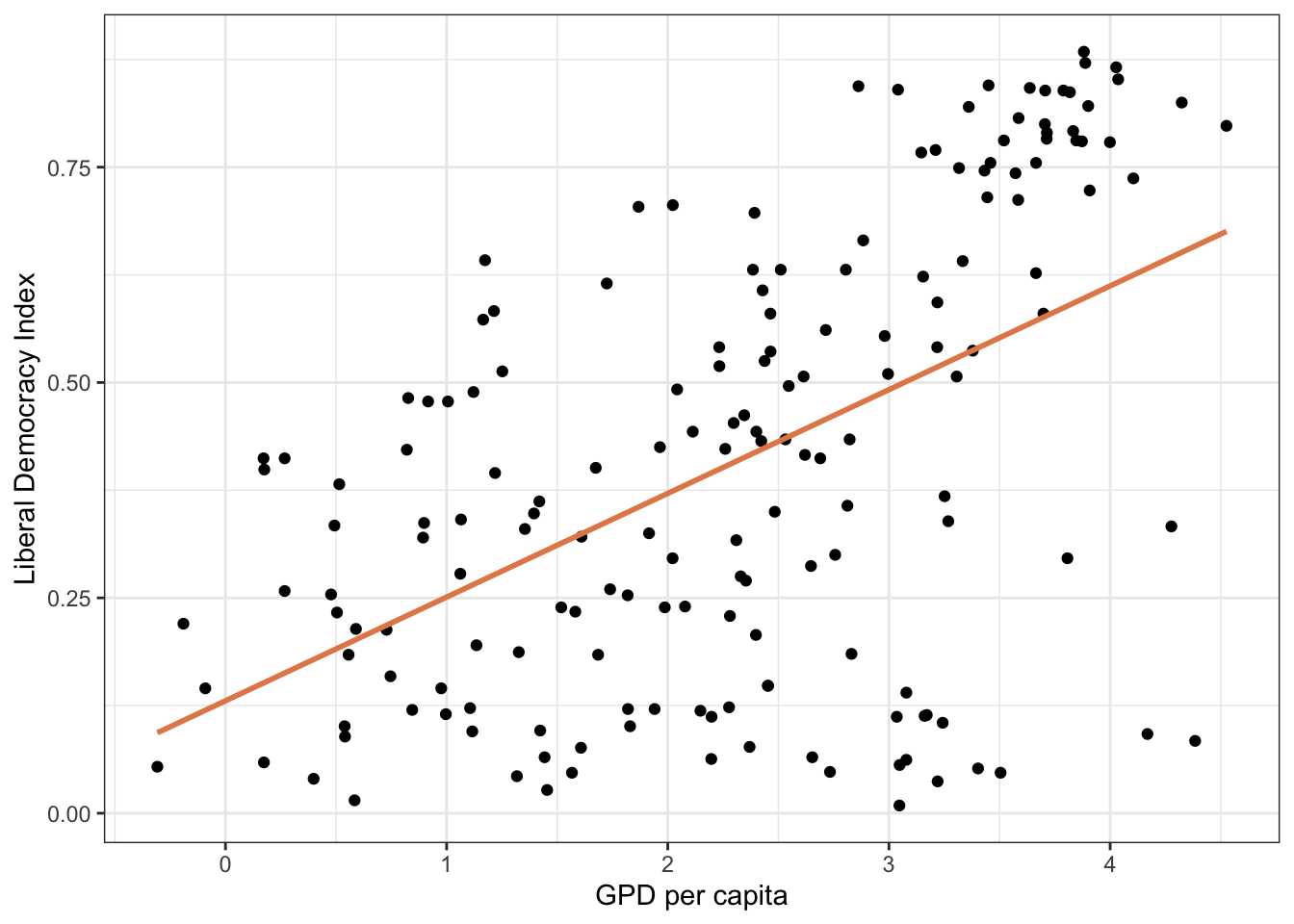
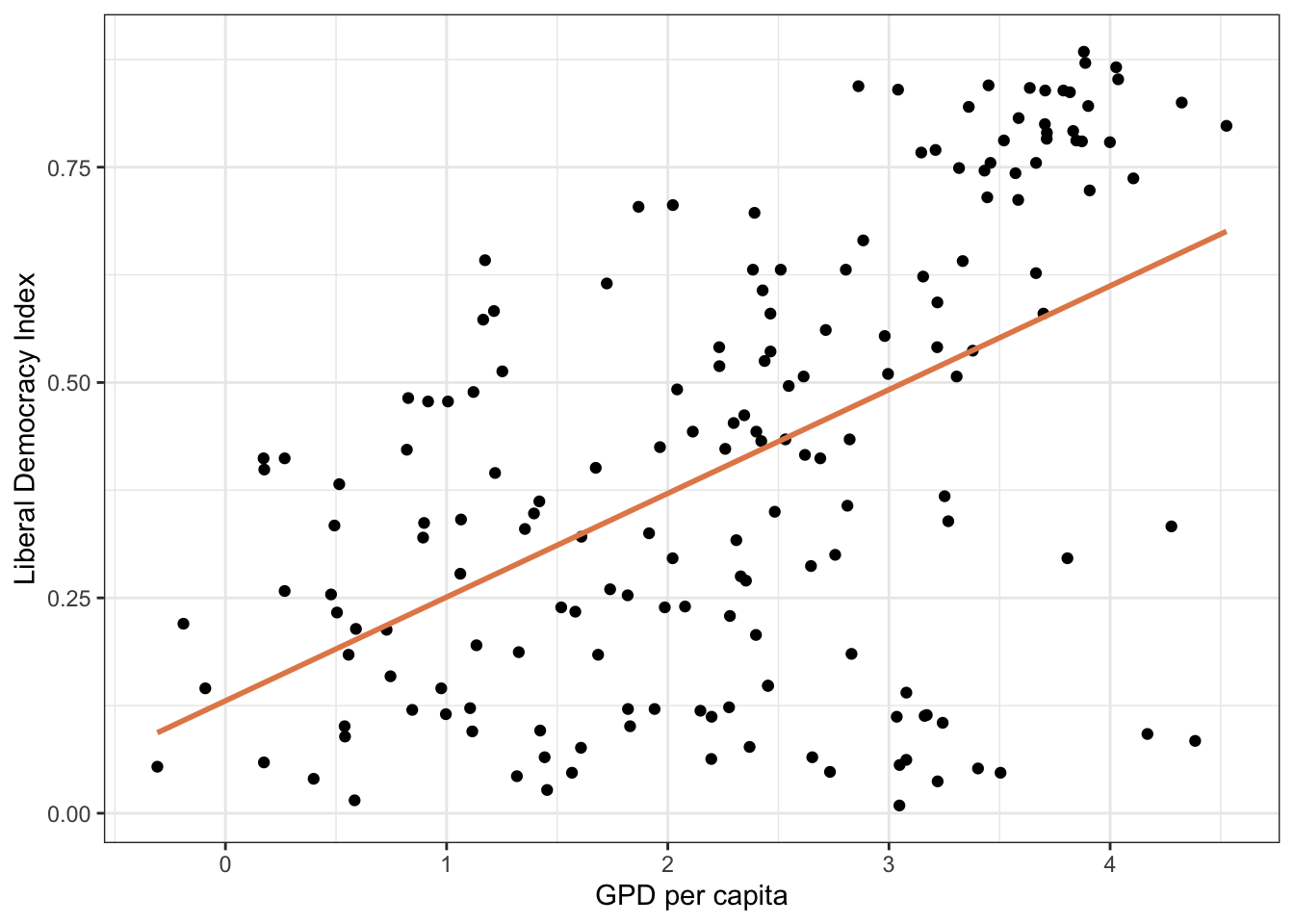
library(vdemdata)
modelData <- vdem %>% 
  filter(year == 2019) %>% 
  select(country_name, v2x_libdem, e_gdppc) %>% 
  mutate(lg_gdppc = log(e_gdppc))
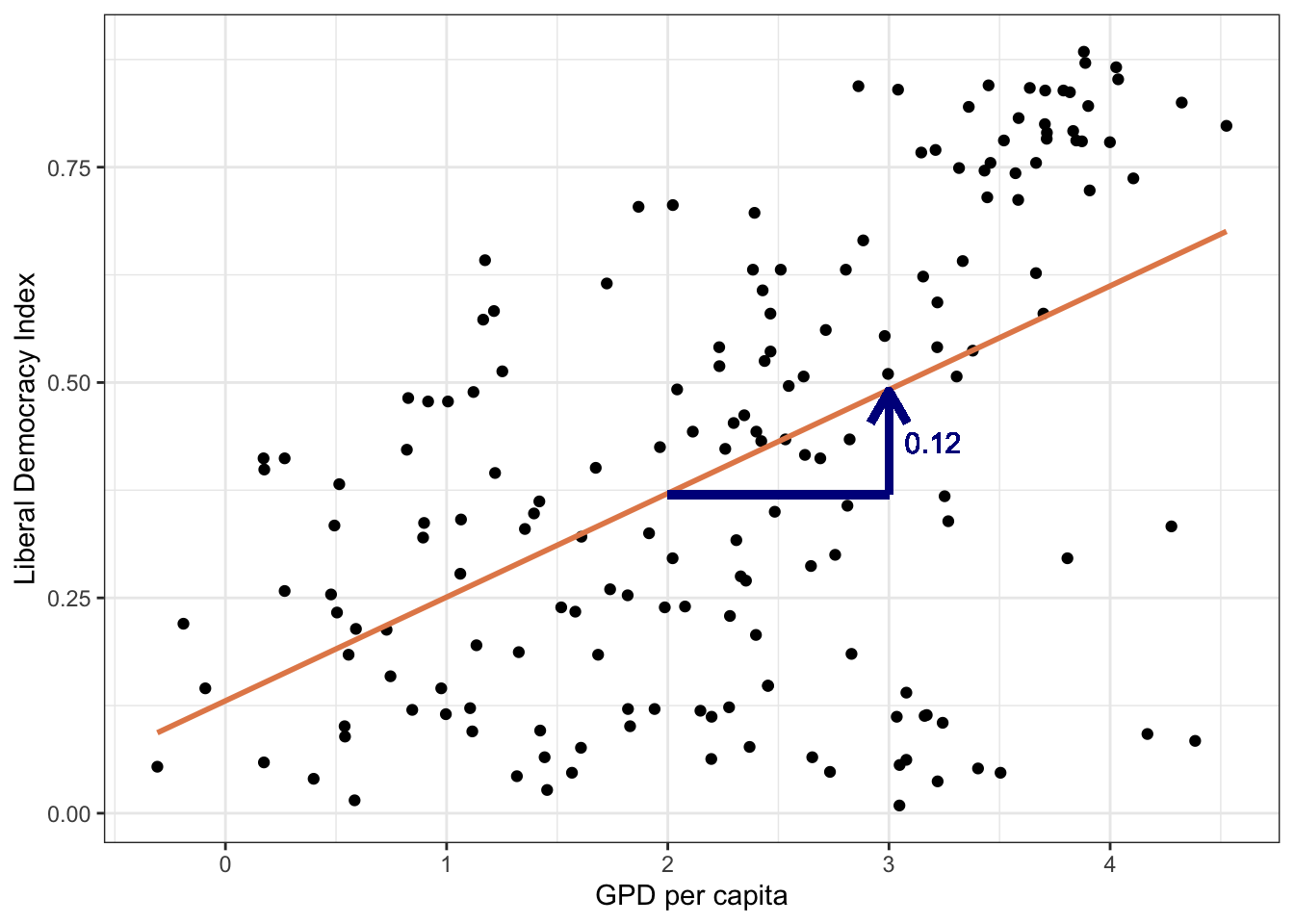
glimpse(modelData)

Rows: 179
Columns: 4
$ country_name <chr> "Mexico", "Suriname", "Sweden", "Switzerland", "Ghana", "…
$ v2x_libdem   <dbl> 0.434, 0.580, 0.871, 0.866, 0.615, 0.607, 0.755, 0.260, 0…
$ e_gdppc      <dbl> 16.814, 11.752, 48.804, 56.110, 5.608, 11.345, 39.061, 5.…
$ lg_gdppc     <dbl> 2.8222119, 2.4640234, 3.8878123, 4.0273140, 1.7241941, 2.…

Visualize first!

Add a trend line

Models as functions

We can represent relationships between variables using functions
A function is a mathematical concept: the relationship between an output and one or more inputs
- Plug in the inputs and receive back the output

Models as functions

Example: The formula is a function with input and output .
- If is , is ,

Language

Response variable: Variable whose behavior or variation you are trying to understand, on the y-axis in the plot
- Dependent variable
- Outcome variable
- Y variable

Language

Explanatory variables: Other variables that you want to use to explain the variation in the response, on the x-axis in the plot
- Independent variables
- Predictors

Linear Model with One Explanatory Variable

is the outcome variable
is the explanatory variable
is the intercept: the predicted value of when is equal to 0
is the slope of the line [remember rise over run!]

Language

Predicted value: Output of the model function
- The model function gives the typical (expected) value of the response variable conditioning on the explanatory variables
- We often call this to differentiate the predicted value from an observed value of Y in the data

Language

Residuals: A measure of how far each case is from its predicted value (based on a particular model)
- Residual = Observed value () - Predicted value ()
- How far above/below the expected value each case is

Residuals

Linear Model

Linear Model: Interpretation

How to interpret our estimate of ?

a is our predicted level of democracy when GDP per capita is 0.

Linear Model: Interpretation

How to interpret our estimate of ?

Linear Model: Interpretation

When :

is the predicted change in associated with a ONE unit change in X.

Linear Model: Interpretation

Is this the causal effect of GDP per capita on liberal democracy?

Correlation vs Causation

The model tells us the association between variables.

There could be reverse or cyclical causation: maybe liberal democracy causes GDP per capita (not vice versa)

There could be an omitted factor (z) that causes both GDP per capita and liberal democracy.
- If true, this is a spurious correlation

Questions for you

An economist is interested in the relationship between years of education (X) and hourly wages in dollars (Y). They estimate a linear model with estimates of and as follows:

Write a sentence to interpret the estimate of (the intercept)
Write a sentence to interpret the estimate of (the slope, or coefficient on YrsEducation)
What is the predicted hourly wage for those with 10 years of education?
Should you interpret this as a causal effect of education? Why or why not?

Intercept

The model predicts that people with years of education will make 9 dollars an hour.

Slope

The model predicts that a one year increase in years of education will result in an additional 1.60 dollars per hour in earnings.

Predicted Hourly Wage for 10 yrs Education

9 + 1.6*10

[1] 25

Next step

Linear model with one predictor:
How do we figure out what the best values are for and ??