Linear Regression Model Specification (regression)
Computational engine: lm Linear Regression 1
Estimation
May 19, 2025
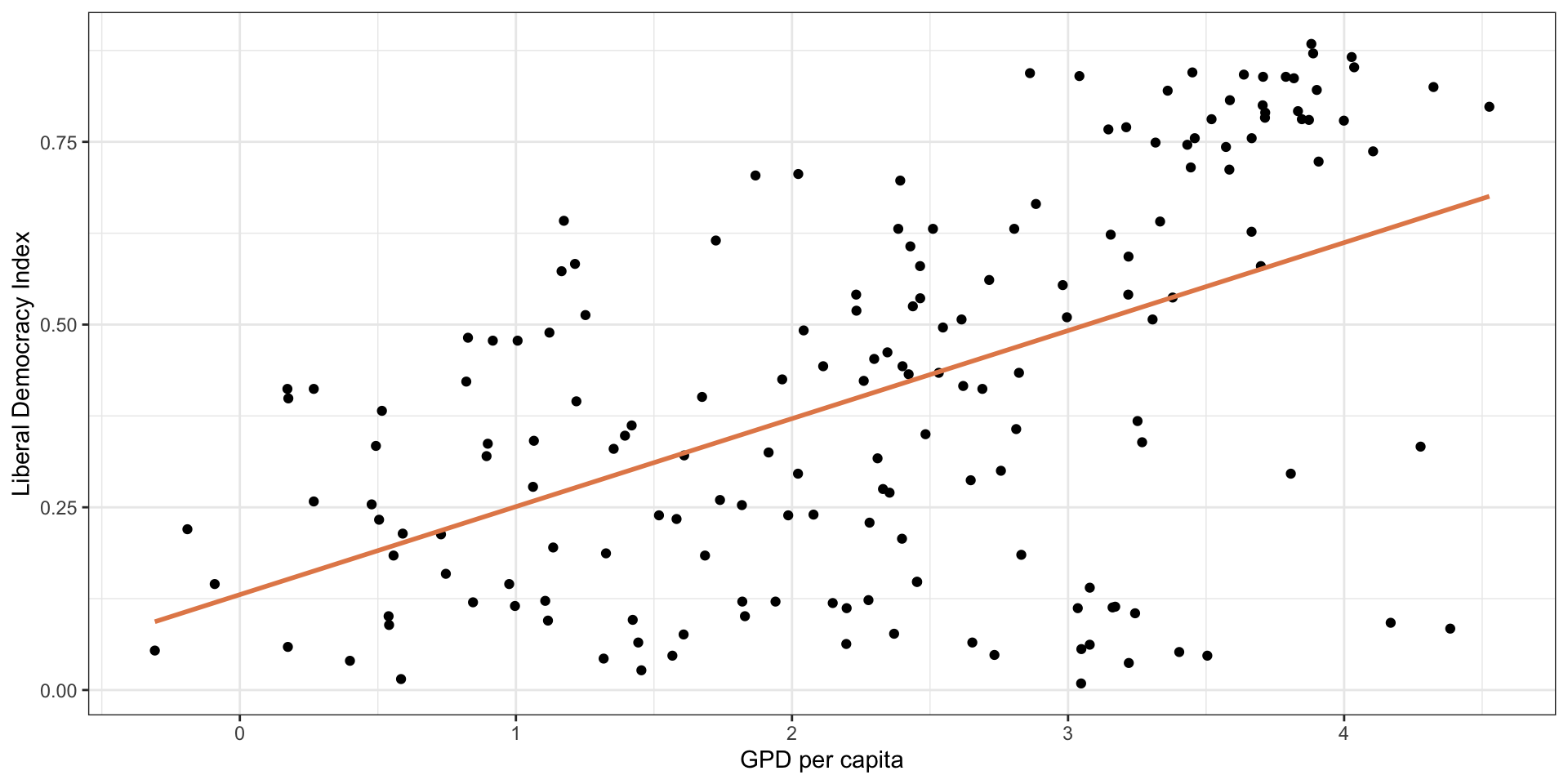
Linear Model with Single Predictor
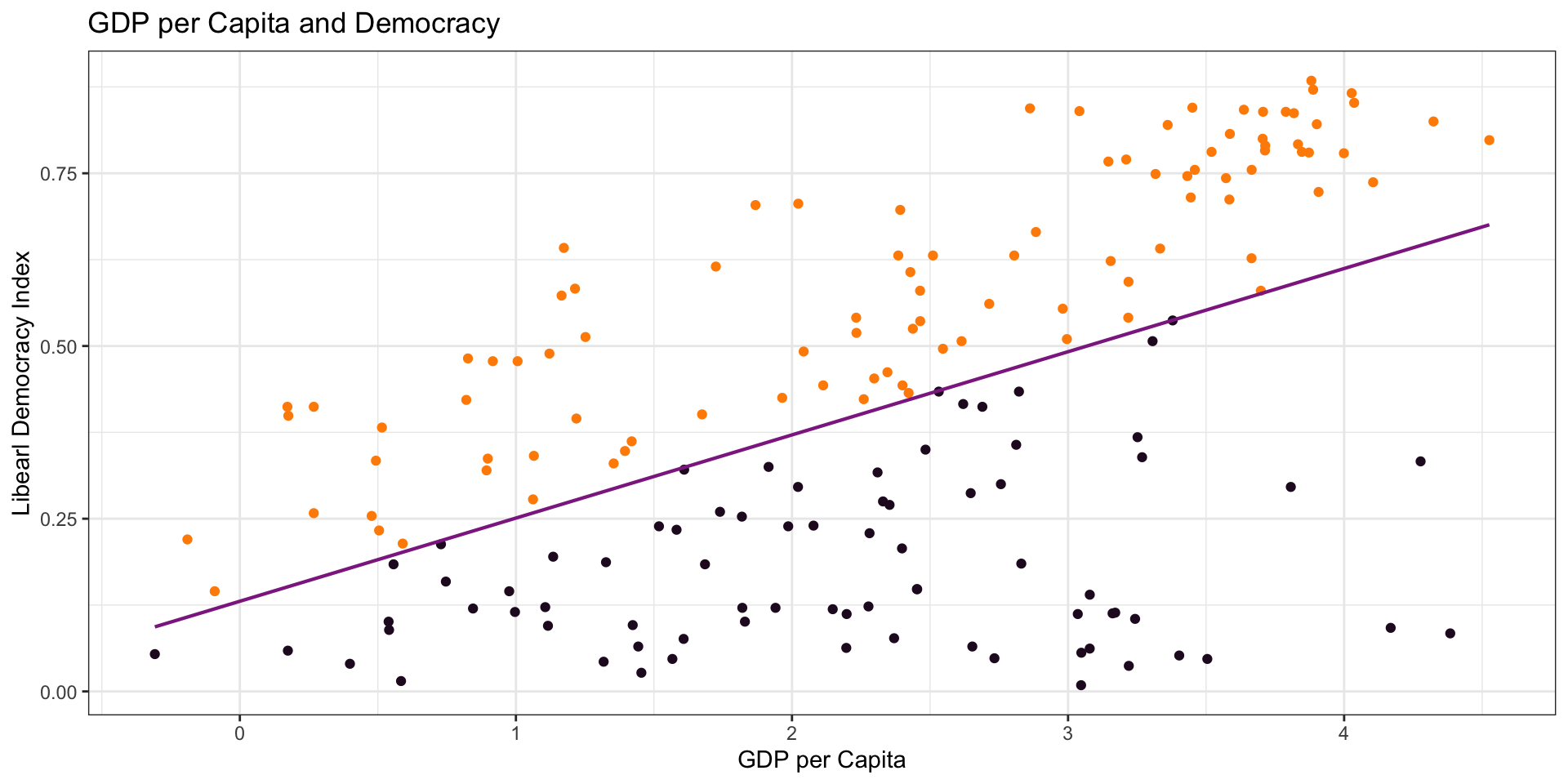
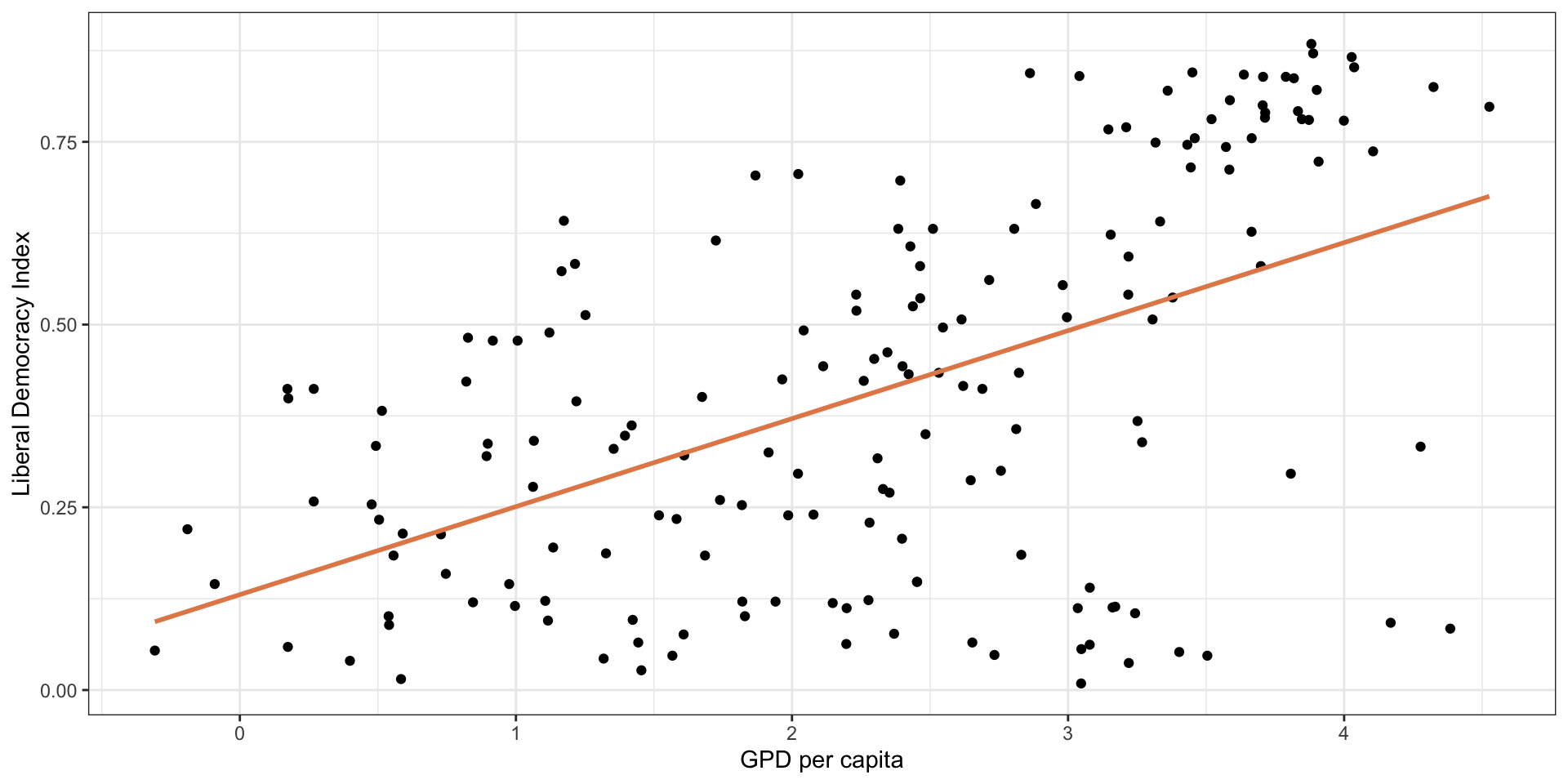
Goal: Estimate Democracy score (\(\hat{Y_{i}}\)) of a country given level of GDP per capita (\(X_{i}\)).
Or: Estimate relationship between GDP per capita and democracy.
Linear Model with Single Predictor
Estimate Model using Tidymodels
Step 1: Specify model
Step 2: Set model fitting engine
Step 3: Fit model & estimate parameters
… using formula syntax
Step 4: Tidy things up…
Estimates
\[\widehat{Democracy}_{i} = 0.13 + 0.12 * {LOGGDPPC}_{i}\]
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.131 0.0381 3.43 7.58e- 4
2 lg_gdppc 0.120 0.0147 8.19 5.75e-14Interpretation?
\[\widehat{Democracy}_{i} = 0.13 + 0.12 * {LOGGDPPC}_{i}\]
Question
How do we get the “best” values for the slope and intercept?
How would you draw the “best” line?
What principle(s) or rules would you use to draw the best line for this relationship?
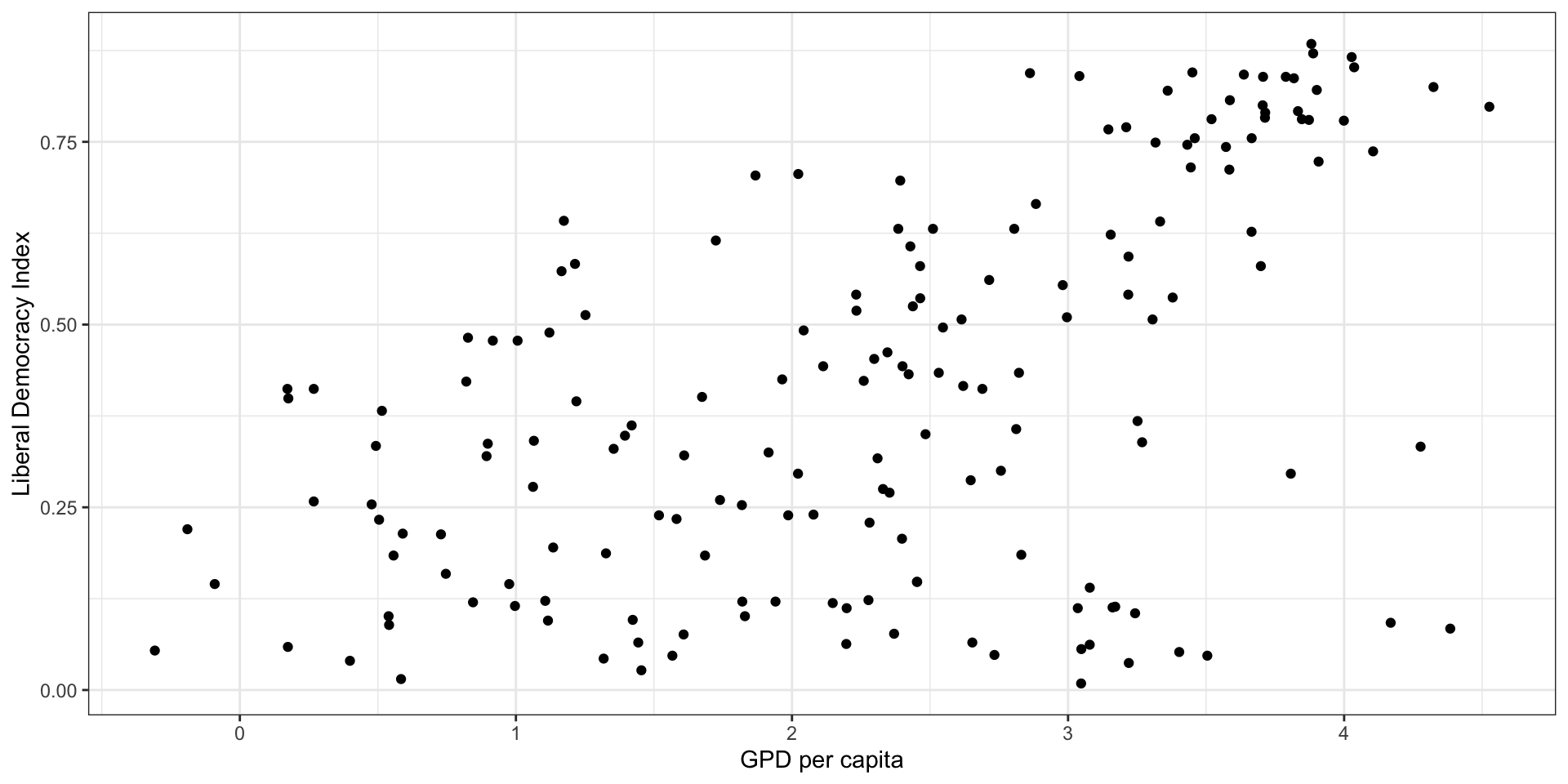
How would you draw the “best” line?
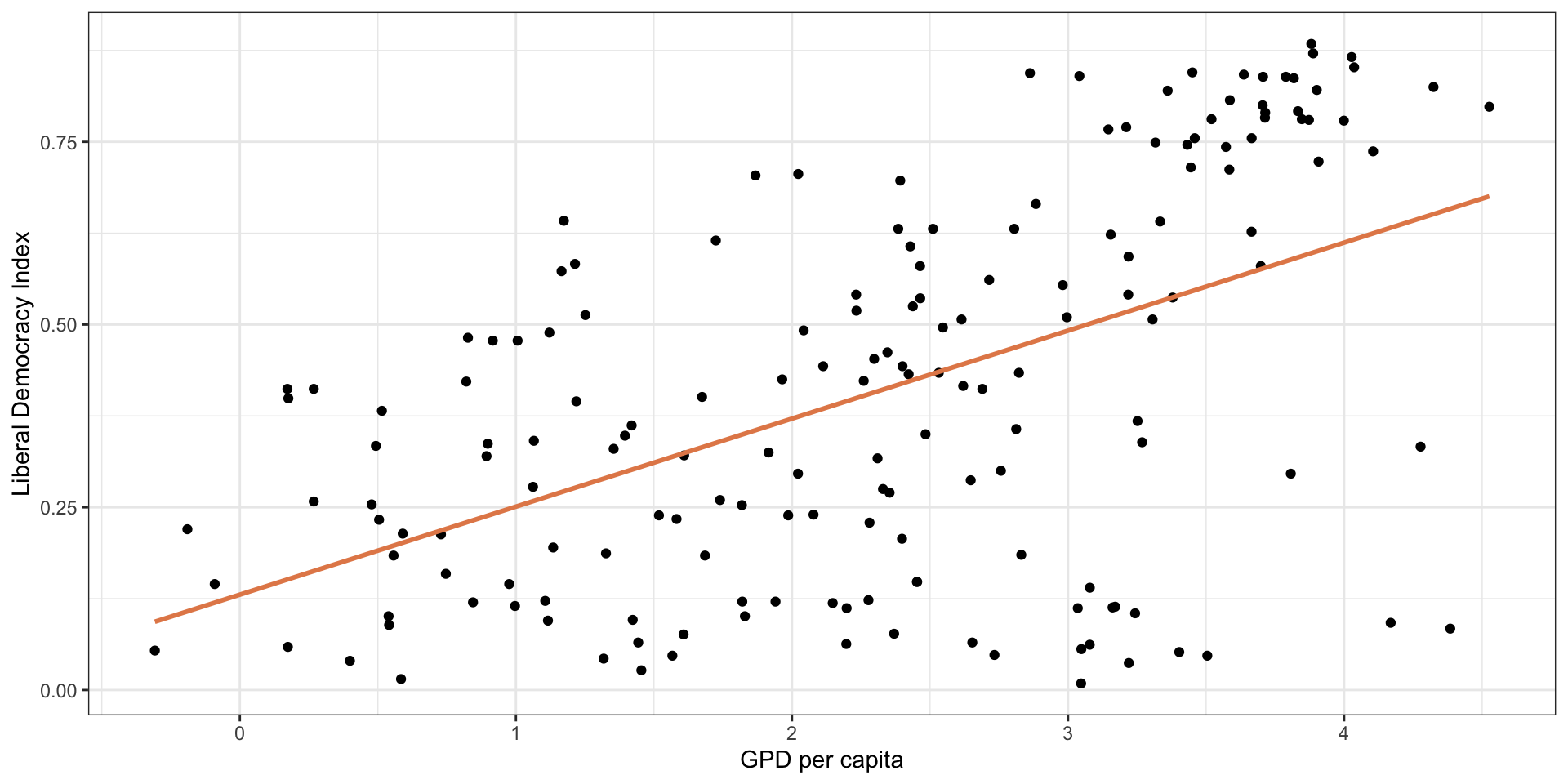
Least squares regression
- Remember the residual is the difference between the actual value and the predicted value
- The regression line minimizes the sum of squared residuals.
Least squares regression
Residual for each point is: \(e_i = y_i - \hat{y}_i\)
Least squares regression line minimizes \(\sum_{i = 1}^n e_i^2\).
Least squares regression
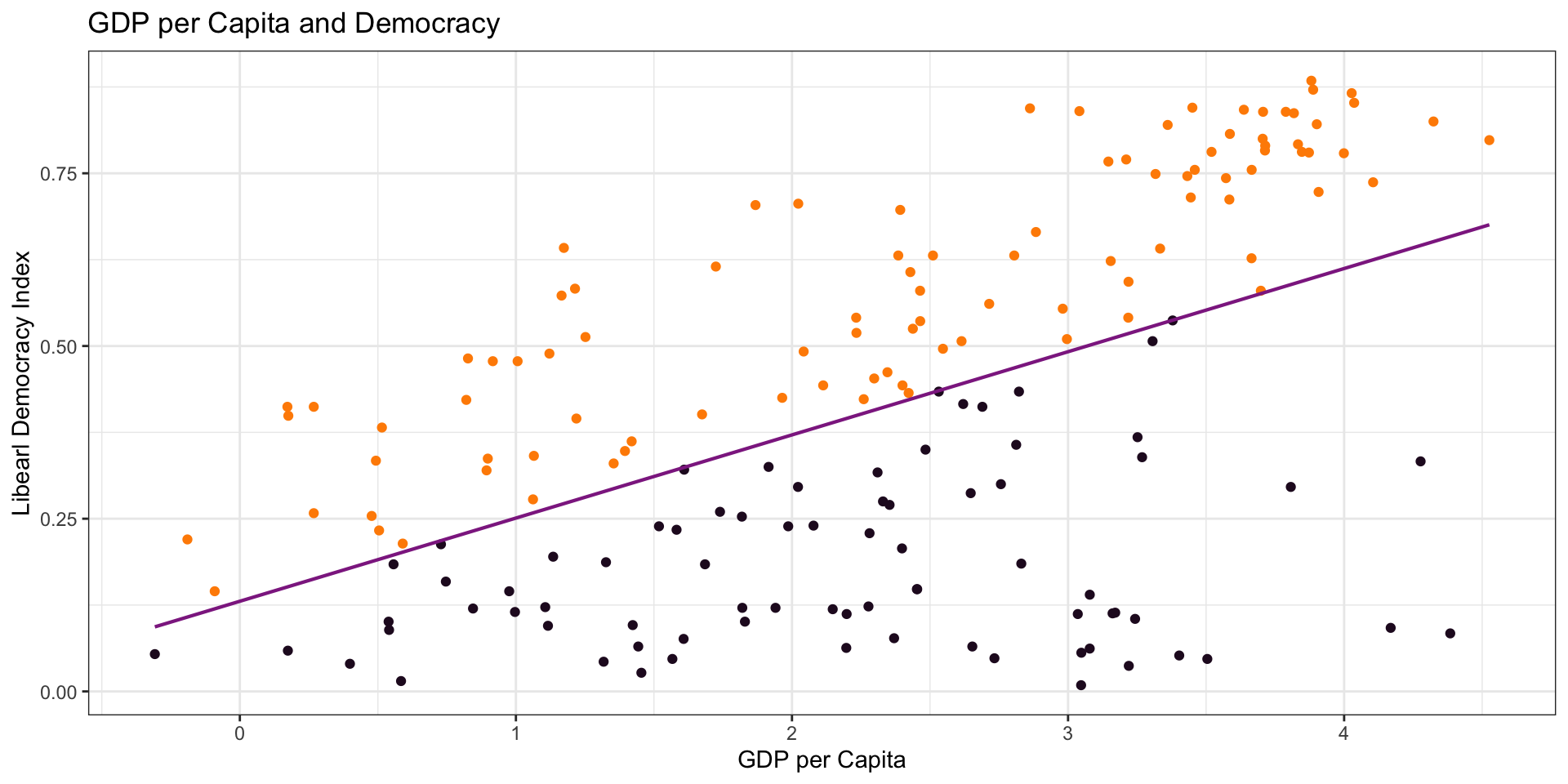
Least Squares Regression
- Why do we square the residual?
Why not take absolute value?
- Principle: larger penalty for residuals further away
- Math: makes the math easier and some nice properties (not our concern here…)
Least squares regression
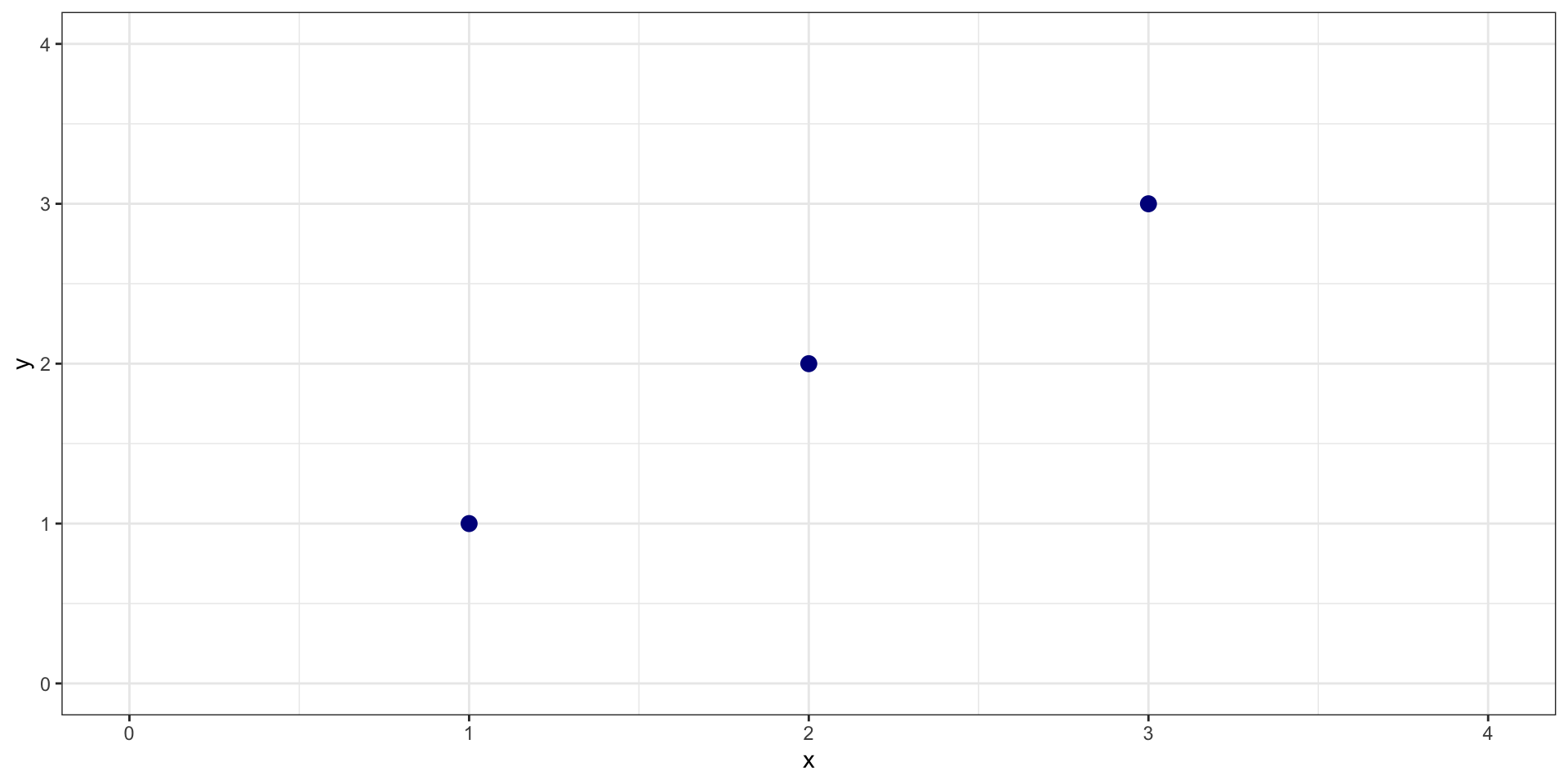
Very Simple Example
What should the slope and intercept be?
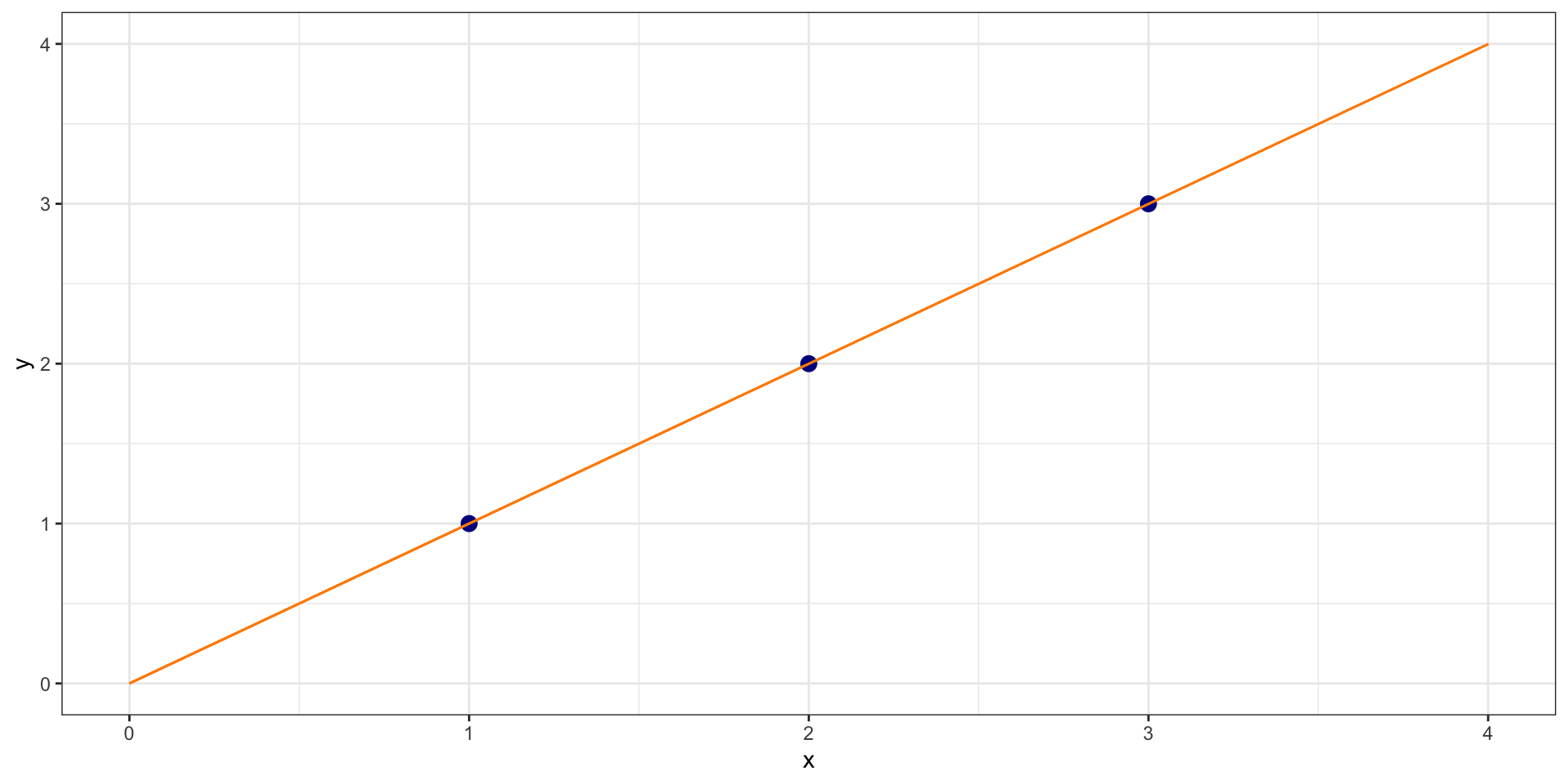
Example
\(\hat{Y} = 0 + 1*X\)
Example
What is the sum of squared residuals?
Example
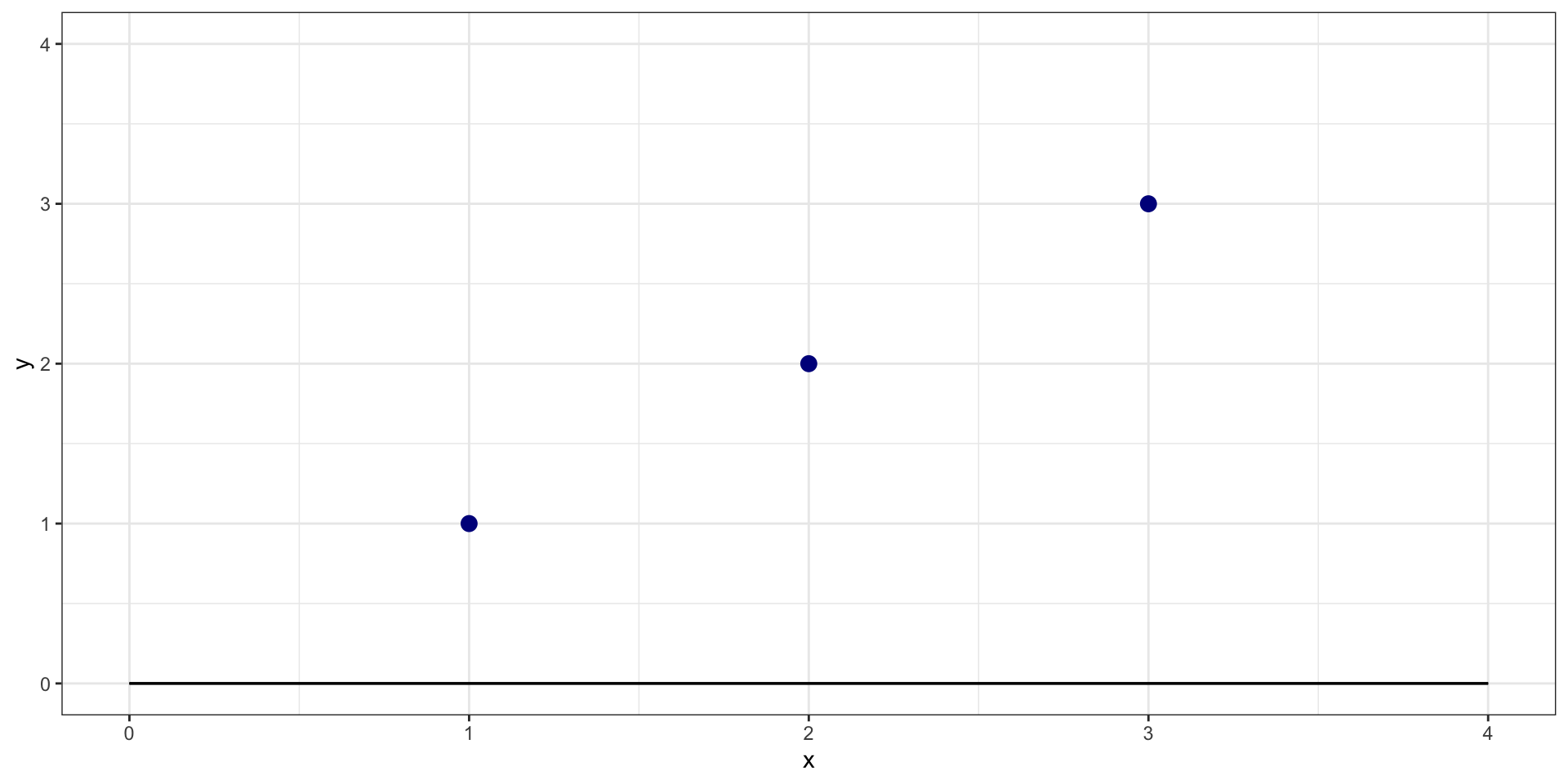
What is sum of squared residuals for \(y = 0 + 0*X\)?
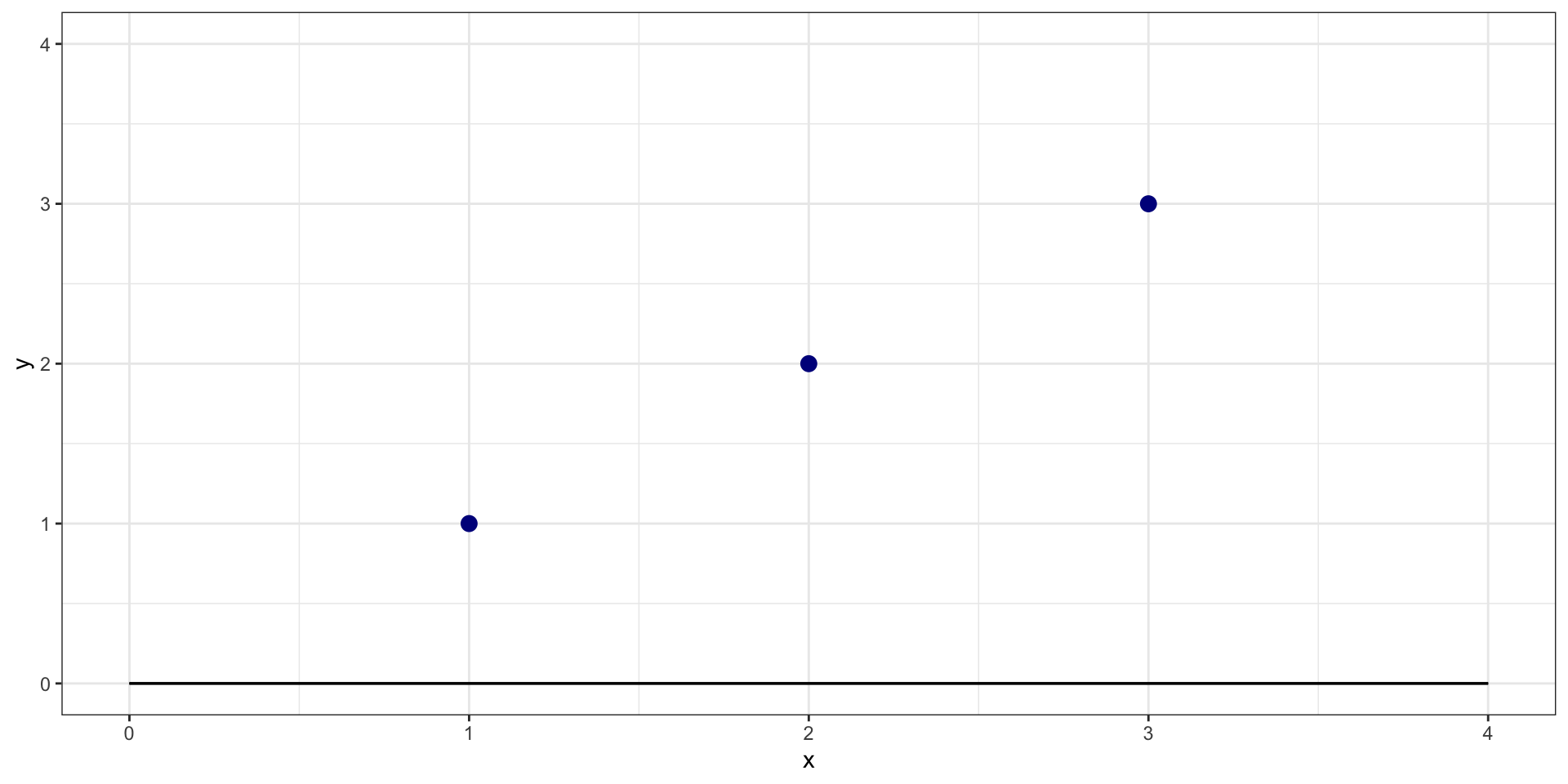
Example
What is sum of squared residuals for \(y = 0 + 0*X\)?
Example
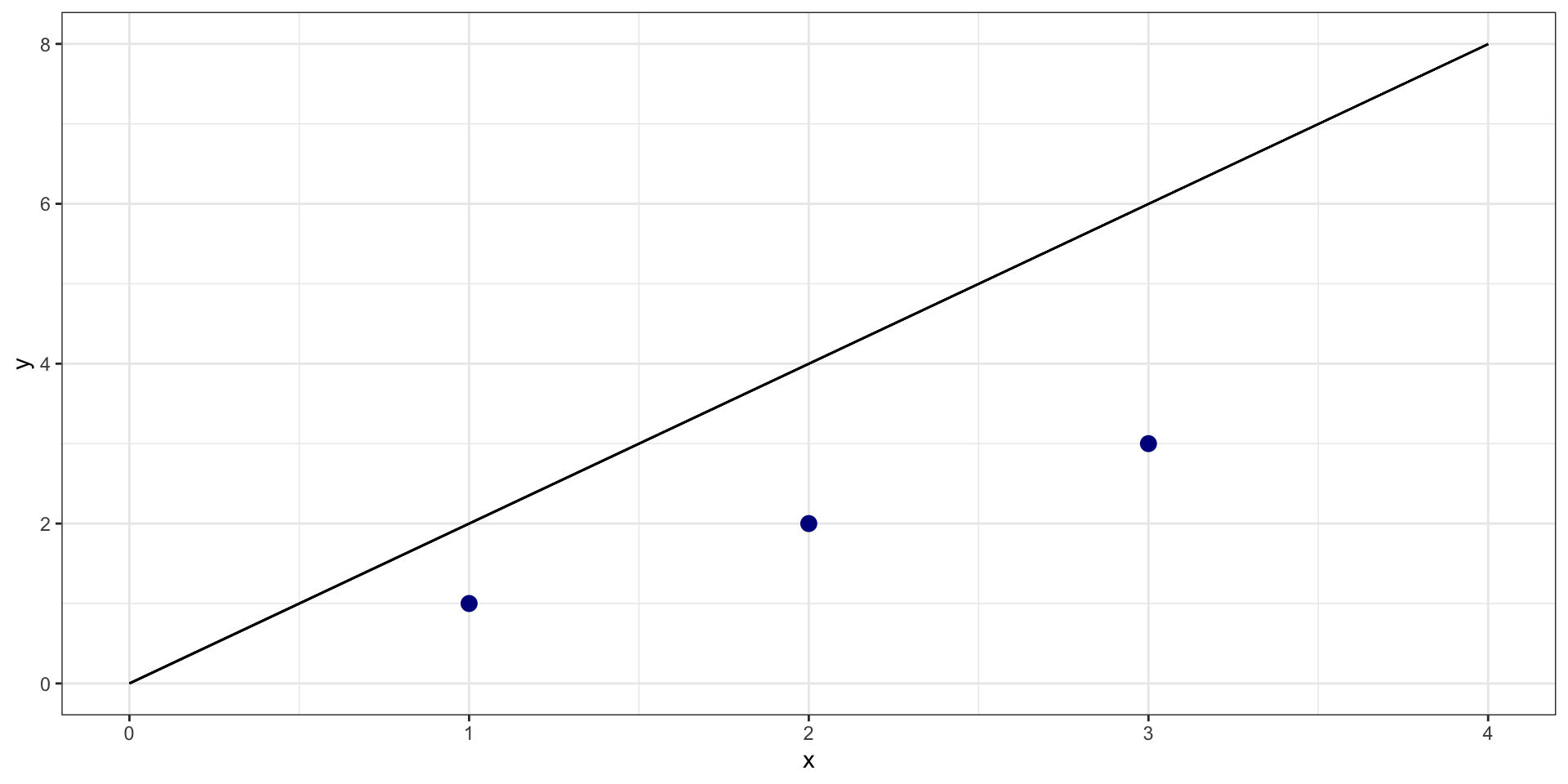
What is sum of squared residuals for \(y = 0 + 2*X\)?
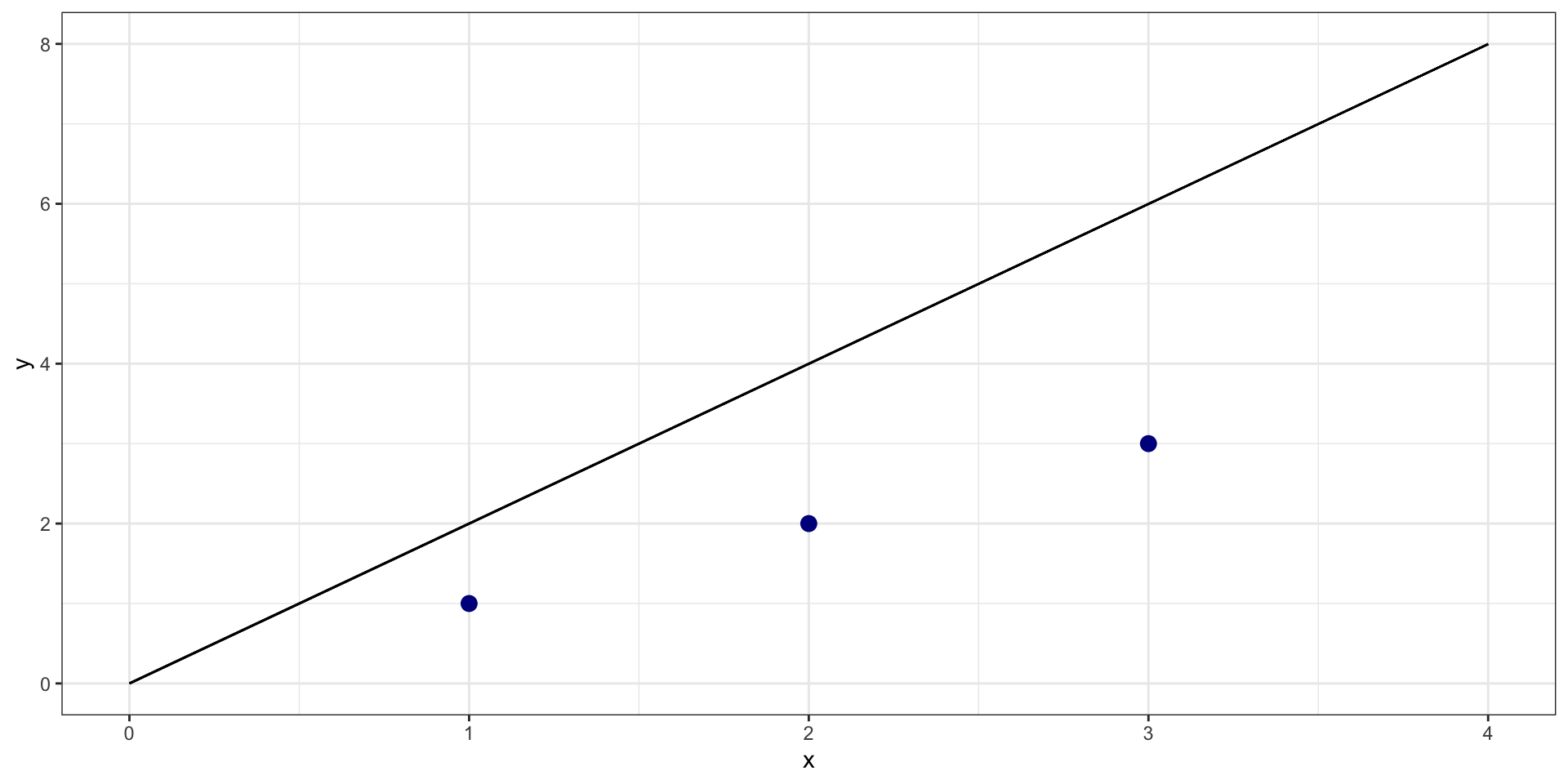
Example
What is sum of squared residuals for \(y = 0 + 2*X\)?
One more…
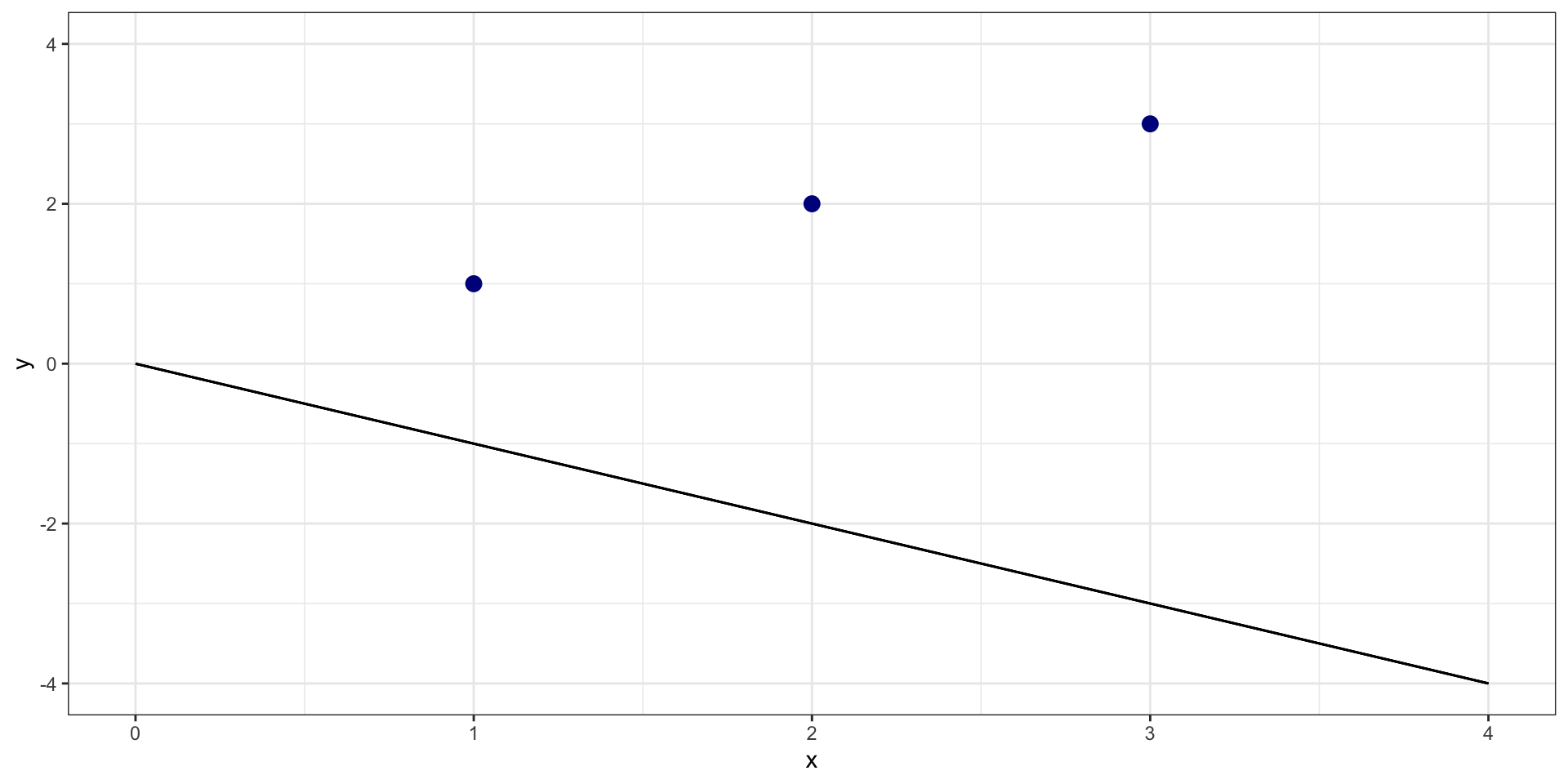
What is sum of squared residuals for \(y = 0 + -1*X\)?
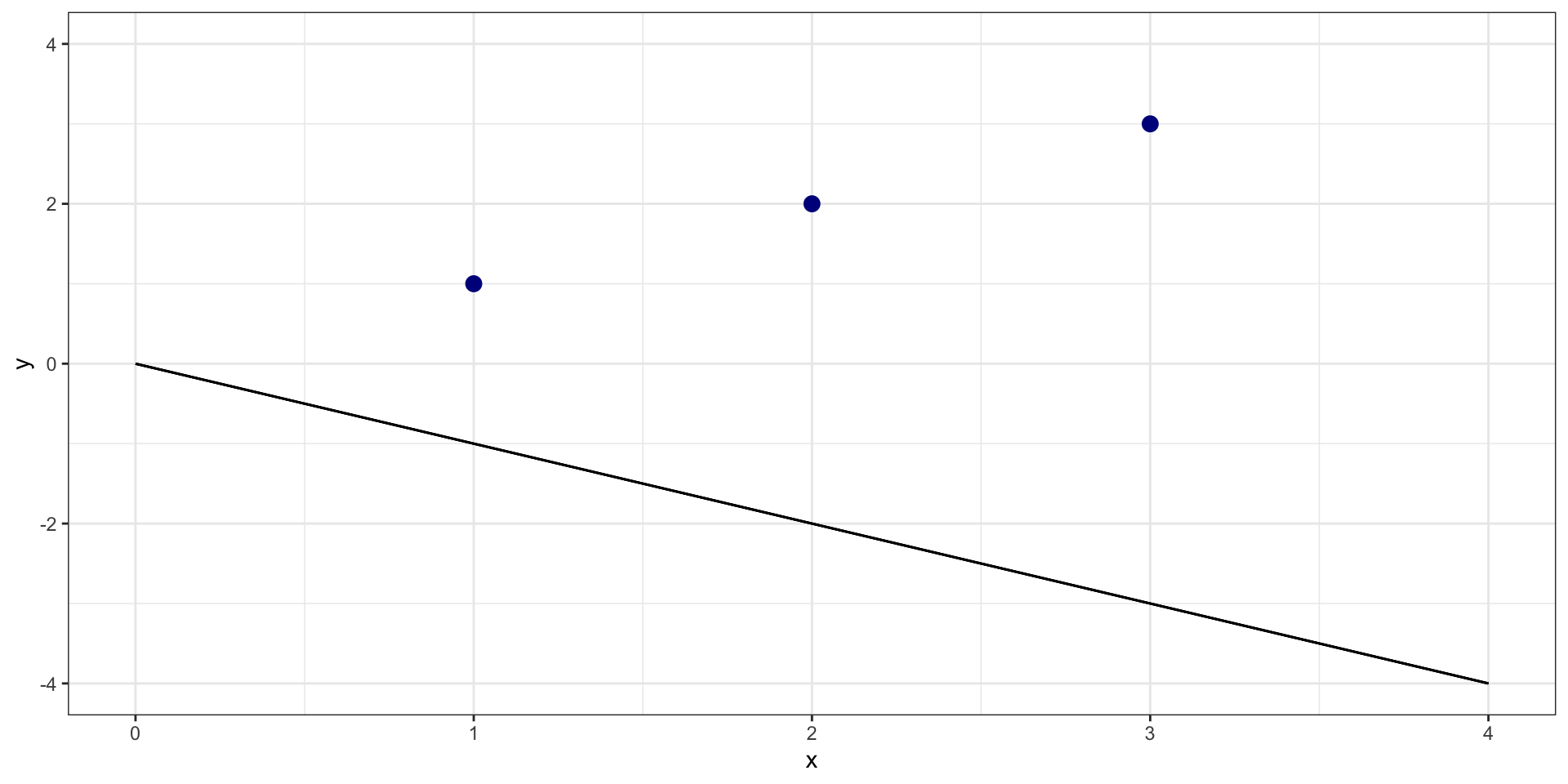
One more…
What is sum of squared residuals for \(y = 0 + -1*X\)?
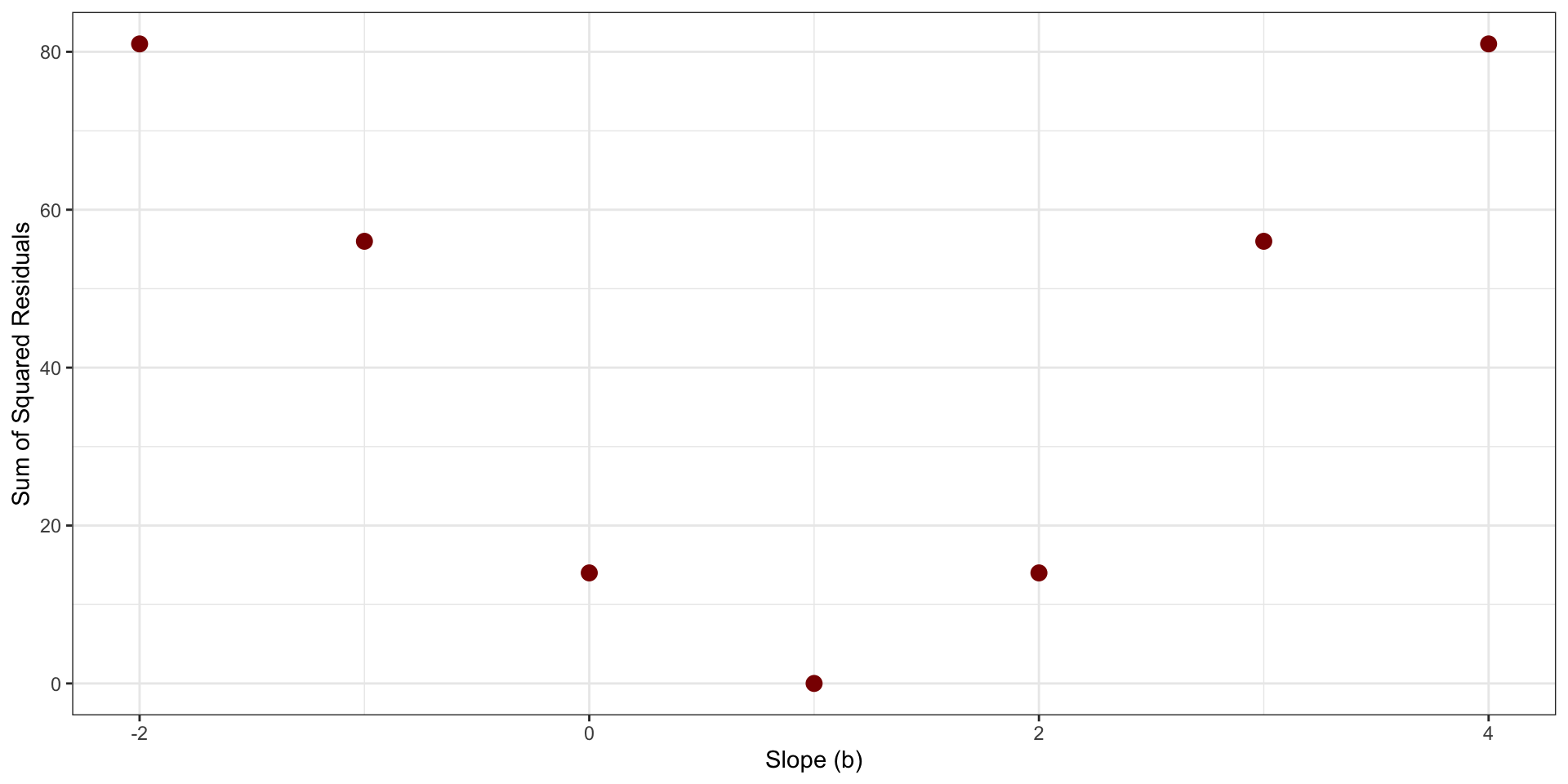
Cost Function
Sum of Squared Residuals as function of possible values of \(b\)
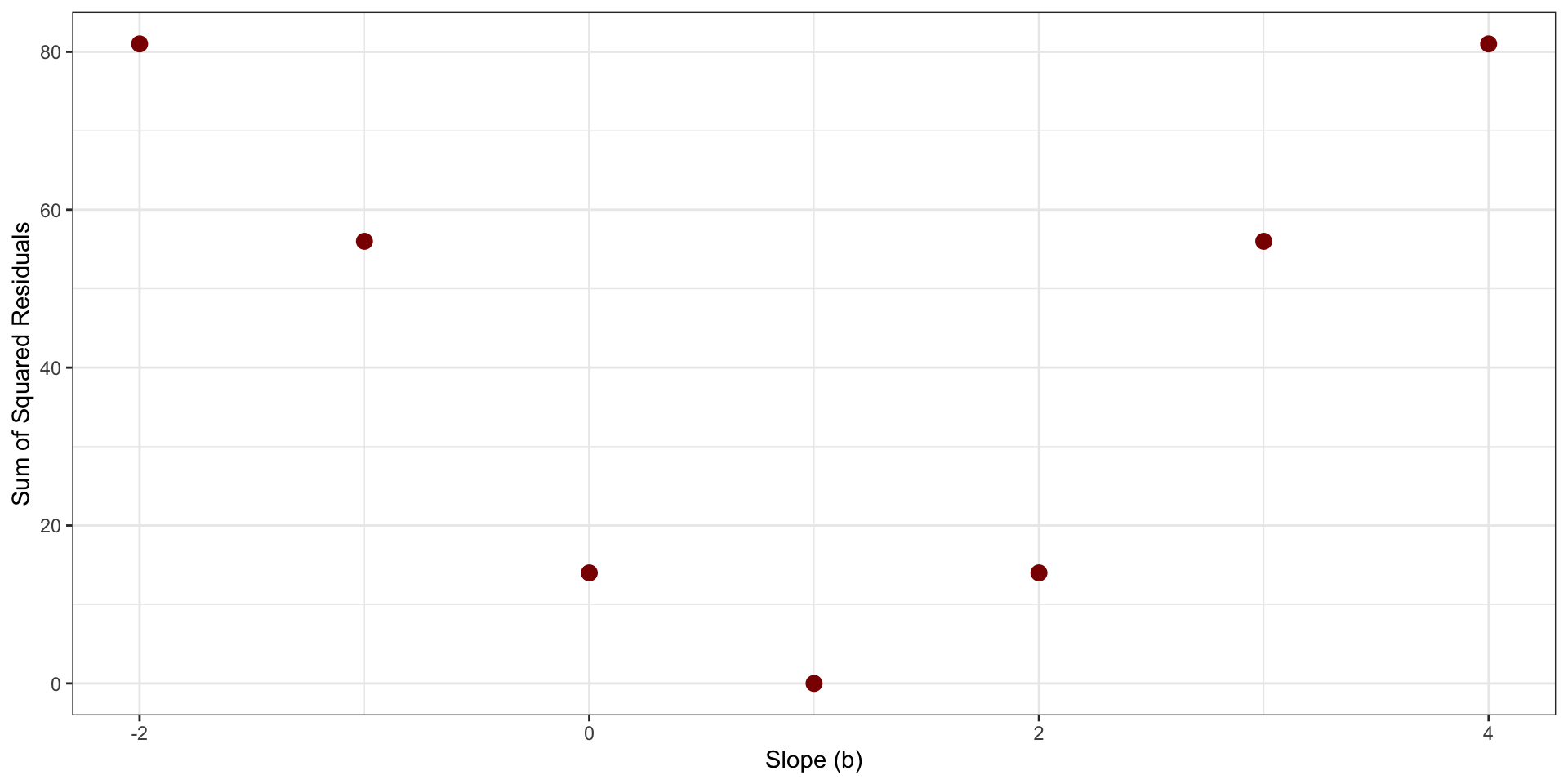
Least Squares Regression
When we estimate a least squares regression, it is looking for the line that minimizes sum of squared residuals
In the simple example, I set \(a=0\) to make it easier. More complicated when searching for combination of \(a\) and \(b\) that minimize, but same basic idea
Least Squares Regression
There is a way to solve for this analytically for linear regression (i.e., by doing math…)
– They made us do this in grad school…
- In machine learning, people also use gradient descent algorithm in which the computer searches over possible combinations of \(a\) and \(b\) until it settles on the lowest point.
Least Squares Regression
Least Squares Regression
Are Democracies Less Corrupt?
Posit Cloud
Models with categorical explanatory variables
Judicial Review and Democracy
Judicial Review:
Do high courts (Supreme Court, Constitutional Court, etc) have the power to rule on whether laws or policies are constitutional/legal? [Yes or No]
Dimension of Judicial Independence
Judicial review and democracy
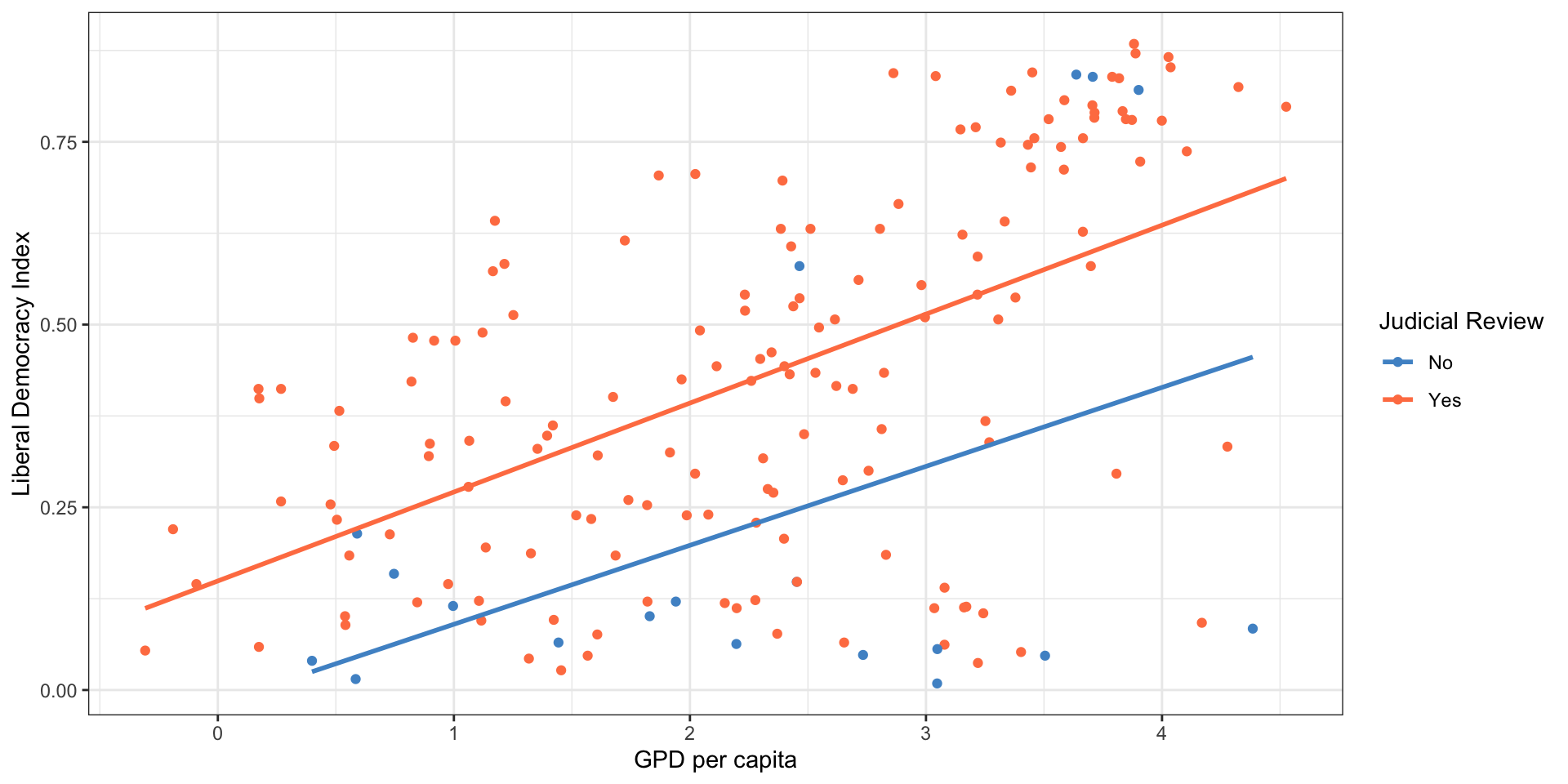
Judicial review (Yes or No) and democracy
Judicial review and democracy
\[\widehat{Democracy_{i}} = 0.22 + 0.20*JudicialReview(yes)\] - Intercept: Countries without judicial review are, on average, a 0.22 on liberal democracy scale
- Slope: Countries with judicial review are expected, on average, to be 0.20 units more democratic on the liberal democracy index
- Compares baseline level (Judicial Review = 0) to the other level (Judicial Review = 1)
Dummy variables
When the categorical explanatory variable has many levels, they’re encoded to dummy variables
We always leave one category out of the model, as the omitted reference category
Each coefficient describes the expected difference between level of the factor and the baseline level
Everything is relative to the omitted reference category in the model
Corruption and World Region
Does region predict levels of corruption?
Since Eastern Europe is the first category, default in R is to use that as the omitted category in models.
The Model
\[\hat{Corruption} = a + b_1LA + b_2MENA + b_3SSA + b_4West + b_5Asia\]
Corruption and World Region
How should we interpret intercept? How about the coefficient on SSA?
# A tibble: 6 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.501 0.0449 11.2 3.73e-22
2 regionLatin America 0.00918 0.0665 0.138 8.90e- 1
3 regionMENA 0.0729 0.0699 1.04 2.98e- 1
4 regionSSAfrica 0.133 0.0565 2.36 1.94e- 2
5 regionWestern Europe and North America -0.439 0.0673 -6.52 7.35e-10
6 regionAsia and Pacific 0.00290 0.0646 0.0449 9.64e- 1Corruption and World Region
What if you want a different baseline category? How do we interpret now?
# make SS Africa the reference category
modelData <- modelData %>%
mutate(newReg = relevel(region, ref=4))
linear_reg() %>%
set_engine("lm") %>%
fit(v2x_corr ~ newReg, data = modelData) %>%
tidy()# A tibble: 6 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.635 0.0344 18.4 1.08e-42
2 newRegEastern Europe -0.133 0.0565 -2.36 1.94e- 2
3 newRegLatin America -0.124 0.0600 -2.07 3.98e- 2
4 newRegMENA -0.0605 0.0637 -0.949 3.44e- 1
5 newRegWestern Europe and North America -0.572 0.0608 -9.41 3.07e-17
6 newRegAsia and Pacific -0.131 0.0578 -2.26 2.52e- 2Which types of regime have more corruption?
V-Dem also includes a categorial regime variable: Closed autocracy (0), Electoral Autocracy (1), Electoral Democracy (2), Liberal Democracy (3)
Back to Posit Cloud
